为什么理想的色谱峰近似于正态分布曲线？

发表于 2025-07-23 Waline：

我们知道理想色谱峰是对称。但如果具体去了解相关内容，通常会告诉我们理想的色谱峰不仅是对称的，更是近似于正态分布曲线。以人民卫生出版社《分析化学》第 8 版为例：

正常色谱峰为对称形正态分布曲线，曲线有最高点，以此点的横坐标为中心，曲线对称地向两侧快速、单调下降。

那么，该如何理解“理想的色谱峰近似于正态分布曲线”呢？

大量随机过程的叠加

首先我们假设没有色谱柱的存在。当我们足够快地向流路中注入化合物，化合物被迅速洗脱，并被检测器检测到。因为我们注入速度和洗脱速度足够快，色谱峰是一条 \(t=0\) 竖线。

当我们在流路中加入色谱柱时，化合物分子与色谱柱会发生各种作用，正是这些作用导致化合物分子保留时间 \(t>0\)，但这些作用并不是必然发生的（如在某一瞬间，有的分子被固定相保留，有的分子在流动相中）。

大量这样的随机过程（事实上，这些随机过程可以用速率理论解释）的叠加，使色谱峰最终呈正态分布曲线。

当然，我们也可以从塔板理论来推导”为什么理想的色谱峰近似于正态分布曲线“。

设容量因子 \(k=\frac{m_s}{m_m}=\frac{q}{p}\)，且 \(p+q=1\)，其中 \(p\) 可以理解为 1 个化合物分子完成一次分配后，存在于流动相中而不被固定相截留（保留）的概率。

当 1 个化合物分子，经过 \(n\) 个塔板分配后，假设其中有 \(r\) 次没有被固定相截留，其发生概率满足二项分布：

\[P(X=r)=C_{n}^{r}\cdot p^{r}\cdot (1-p)^{n-r}\]

\(P(X=r)\) 表示在 \(n\) 次独立重复的伯努利试验（只有两种可能结果的单次随机试验）中，所期望的事件恰好发生 \(r\) 次的概率。

当 1 个化合物分子在 \(n\) 次分配中，有 \(r\) 次通过塔板，最终就会存在于第 \(r\) 号的塔板内。因此，当有大量的分子时同时注入色谱柱时，化合物在空间分布上的分布也近似于二项分布概率密度函数。

当 \(p\neq0.5\) 时，二项分布概率密度函数是偏倚的，随着 \(n\) 值增大，分布逐渐趋于对称。棣莫弗－拉普拉斯定理（De Moivre–Laplace theorem）指出，当 \(n\to\infty\) 时，二项分布趋近于正态分布。

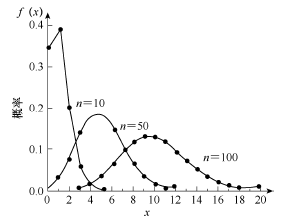
Figure 1. \(n\) 值不同的二项分布

因此，当塔板数足够大（如 \(n>2000\)）时，色谱峰近似于正态分布曲线。