酶促反应动力学
酶动力学基本参数
米氏方程
1902 年 Victor Henri 提出了酶- 底物中间复合物学说,认为首先是酶 E 与底物 S 生成酶-底物 中间复合物 ES,然后 ES 分解生成产物 P 和游离的酶。
\[ \ce{E + S <=>[k_1][k_2] ES ->[k_3] E + P} \]
式中的 \(k_{1}\)、\(k_{2}\) 和 \(k_{3}\) 分别为各向反应的速率常数。
1913 年 Leonor Michaelis 和 Maud Menten 根据酶-底物复合物学说,经过大量实验,得出表示酶促反应动力学基本原理的数学表达式,即单底物浓度 \([S]\) 与酶反应速度 \(v\) 的定量关系,即著名的米-门二氏方程(Michaelis-Menten equation,也称米氏方程)。
\[ v = \frac{V_{max} [S]}{K_{m} + [S]} \]
- \(v\) 指酶促反应的速率;
- \(V_{max}\) 指酶促反应的最大反应速率;
- \(K_{m}\) 是底物的米氏常数,\(K_{m} = \frac{k_{2}+k_{3}}{k_{1}}\)。
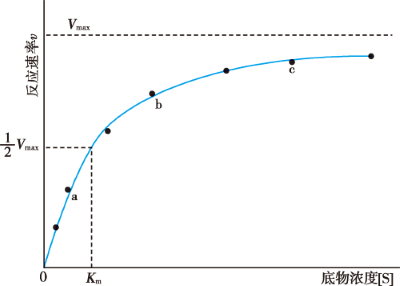
Figure 1. 底物浓度对酶促反应速率的影响
可知如下重要性质:
- \(K_{m}\) 值等于酶促反应速率为最大反应速率一半时的底物浓度;
- \(K_{m}\) 值是酶的特征性常数,\(K_{m}\) 值的大小并非固定不变,它与酶的结构、底物结构、反应环境的 pH、温度和离子强度有关,而与酶浓度无关;
- \(K_{m}\) 在一定条件下可表示酶对底物的亲和力;
- \(V_{max}\) 是酶被底物完全饱和时的反应速率。
酶动力学参数的测定
要测量 \(K_{m}\) 和 \(V_{max}\) 值,可以通过测量一系列不同底物浓度 \([S]\) 及对应的初始反应速率 \(v\),然后使用林-贝作图法(Lineweaver-Burk plot)或直接拟合进行求解。
Lineweaver-Burk plot
将米氏方程的两边同时取倒数,有:
\[\frac{1}{v}=\frac{K_{m}}{V_{\max}}\cdot\frac{1}{[\mathrm{S}]}+\frac{1}{V_{\max}}\]
以 \(\frac{1}{v}\) 对 \(\frac{1}{[S]}\) 作图,纵轴上的截距为 \(\frac{1}{V_{max}}\),横轴上的截距为 \(-\frac{1}{K_{m}}\),称为林-贝作图法(Lineweaver-Burk plot)。
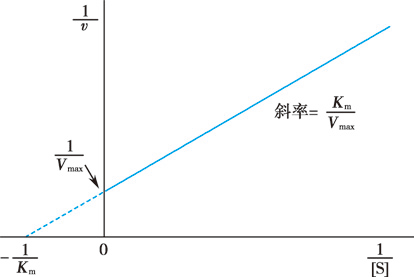
Figure 2. 林-贝作图法(Lineweaver-Burk plot)
抑制常数
\[ \ce{E + I <=> EI} \]
抑制常数(Inhibitory constant, \(K_i\))即抑制剂-酶复合 EI 解离为游离酶 E 和抑制剂 I 的解离常数,\(K_i\) 反应抑制剂与酶的亲和力强度,\(K_i\) 越小,表明抑制剂与酶的亲和力越强。
\[ K_i=\frac{[E][I]}{[EI]} \]
\(K_i\) 在一定条件下(如特定的温度、pH 和缓冲液体系等)是常数,而与酶浓度 \([E]\) 和 抑制剂浓度 \([I]\) 无关,也与底物存在与否无关。
竞争性抑制
在竞争性抑制(Competitive Inhibition)中,抑制剂 I 与底物 S 竞争酶的同一个活性位点。抑制剂只能与游离的酶 E 结合,不能与酶-底物复合物 ES 结合。
所涉及的化学平衡如下:
- \(\ce{E + S <=> ES -> E + P}\)
- \(\ce{E + I <=> EI}\)
\[v = \frac{V_{max}[S]}{K_m \left( 1 + \frac{[I]}{K_i} \right) + [S]}\]
通过比较可以看出,竞争性抑制剂使表观米氏常数 \(K_m^{app}\) 增加了 \((1 + \frac{[I]}{K_i})\) 倍:
\[K_m^{app} = K_m \left( 1 + \frac{[I]}{K_i} \right)\]
,而 \(V_{max}\) 不变。
非竞争性抑制
在经典的非竞争性抑制(Non-competitive Inhibition)中,抑制剂 I 与底物 S 结合在酶的不同位点上。抑制剂既可以与游离酶 E 结合,也可以与酶-底物复合物 ES 结合,且结合能力相同。
所涉及的化学平衡如下:
- \(\ce{E + S <=> ES -> E + P}\)
- \(\ce{E + I <=> EI}\) (解离常数为 \(K_i\))
- \(\ce{ES + I <=> ESI}\) (解离常数为 \(K_i^{\prime}\),且 \(K_i^{\prime} = K_i\))
- \(\ce{EI + S <=> ESI}\)
\[v = \frac{\frac{V_{max}}{1 + \frac{[I]}{K_i}}[S]}{K_m + [S]}\]
在这种情况下,\(K_m\) 不变,而表观最大反应速度 \(V_{max}^{app}\) 降低了:
\[V_{max}^{app} = \frac{V_{max}}{1 + \frac{[I]}{K_i}}\]
反竞争性抑制
在反竞争性抑制(Uncompetitive Inhibition)中,抑制剂 I 只能与酶-底物复合物 ES 结合,形成无活性的 ESI 复合物。
所涉及的化学平衡如下:
- \(\ce{E + S <=> ES -> E + P}\)
- \(\ce{ES + I <=> ESI}\) (解离常数为 \(K_i^{\prime}\))
通过与竞争性抑制类似的代数变换,最终可以推导出反竞争性抑制下的米氏方程:
\[v = \frac{\frac{V_{max}}{1 + \frac{[I]}{K_i'}}[S]}{\frac{K_m}{1 + \frac{[I]}{K_i'}} + [S]}\]
在这种情况下,\(V_{max}\) 和 \(K_m\) 都受到了影响,它们都除以了同一个因子 \((1+\frac{[I]}{K_i'})\)。
\[V_{max}^{app} = \frac{V_{max}}{1 + \frac{[I]}{K_i'}} \quad \text{and} \quad K_m^{app} = \frac{K_m}{1 + \frac{[I]}{K_i'}}\]
混合型抑制
在混合型抑制(Mixed Inhibition)中,抑制剂不仅可以与游离的酶 E 结合,也可以酶-底物复合物 ES 结合,且抑制剂与这两种形式的酶的亲和力不同。
所涉及的化学平衡如下:
- \(\ce{E + S <=> ES -> E + P}\)
- \(\ce{E + I <=> EI}\) (解离常数为 \(K_i\))
- \(\ce{ES + I <=> ESI}\) (解离常数为 \(K_i^{\prime}\),且 \(K_i^{\prime} \neq K_i\))
- \(\ce{EI + S <=> ESI}\)
混合型抑制的米氏方程:
\[ v=\frac{V_{max}\cdot[S]}{K_m(1+\frac{[I]}{K_i})+[S](1+\frac{[I]}{K_i^{\prime}})} \]
假设:
\[K_i^{\prime}=\alpha\cdot K_i\]
- 如果 \(α>1\),则 \(K_i^{\prime} > K_{i}\),表示抑制剂与游离酶的结合能力更强;
- 如果 \(α<1\),则 \(K_i^{\prime} < K_{i}\),表示抑制剂与酶-底物复合物的结合能力更强。
米氏方程整理为
\[v=\frac{V_{max}\cdot[S]}{K_m(1+\frac{[I]}{K_i})+[S](1+\frac{[I]}{\alpha K_i})}\]
表观最大反应速率 \(V_{max}^{app}\):
\[V_{max}^{app}=\frac{V_{max}}{1+\frac{[I]}{K_i^{\prime}}}=\frac{V_{max}}{1+\frac{[I]}{\alpha K_i}}\]
由于抑制剂可以结合到 ES 复合物上形成无活性的 ESI 复合物,从而降低了有效催化复合物的浓度,因此表观最大反应速率 \(V_{max}^{app}\) 总是减小。
表观米氏常数 \(K_m^{app}\):
\[K_m^{app}=K_m\frac{1+\frac{[I]}{K_i}}{1+\frac{[I]}{K_i^{\prime}}}=K_m\frac{1+\frac{[I]}{K_i}}{1+\frac{[I]}{\alpha K_i}}\]
\(K_m^{app}\) 的变化取决于抑制剂对 E 和 ES 的相对亲和力(即 \(α\) 的值):
- 如果抑制剂优先结合游离酶(\(α>1\)),则 \(K_m^{app}\) 增大(表观亲和力下降)。
- 如果抑制剂优先结合酶-底物复合物(\(α<1\)),则 \(K_m^{app}\) 减小(表观亲和力上升)。
抑制常数的测量
基本思路
基本思路是,通过测量在不同底物浓度 \([S]\) 和不同抑制剂浓度 \([I]\) 条件下酶的反应速率 \(v\),来观察抑制剂对酶动力学参数(\(V_{max}\) 和 \(K_{m}\))的影响。
实验设计:设置一系列抑制剂浓度 \([I]\),每一个固定的抑制剂浓度下,再设置一系列底物浓度 \([S]\) ,测量在不同底物浓度 \([S]\) 和不同抑制剂浓度 \([I]\) 条件下酶初始反应速率 \(v\)。
Table 1. 实验组设计示例
| \([I]_0\) | \([I]_1\) | \([I]_2\) | \([I]_3\) | |
|---|---|---|---|---|
| \([S]_1\) | \(v_{1,0}\) | \(v_{1,1}\) | \(v_{1,2}\) | \(v_{1,3}\) |
| \([S]_2\) | \(v_{2,0}\) | \(v_{2,1}\) | \(v_{2,2}\) | \(v_{2,3}\) |
| \([S]_3\) | \(v_{3,0}\) | \(v_{3,1}\) | \(v_{3,2}\) | \(v_{3,3}\) |
| \([S]_4\) | \(v_{4,0}\) | \(v_{4,1}\) | \(v_{4,2}\) | \(v_{4,3}\) |
| \([S]_5\) | \(v_{5,0}\) | \(v_{5,1}\) | \(v_{5,2}\) | \(v_{5,3}\) |
| \([S]_6\) | \(v_{6,0}\) | \(v_{6,1}\) | \(v_{6,2}\) | \(v_{6,3}\) |
| \([S]_7\) | \(v_{7,0}\) | \(v_{7,1}\) | \(v_{7,2}\) | \(v_{7,3}\) |
结果分析
酶动力学参数
在不加抑制剂一组(\([I]=0\))中,以不同底物浓度 \([S]\) 及对应的初始反应速率 \(v\),使用林-贝作图法(Lineweaver-Burk plot)或直接拟合进行求解 \(K_{m}\) 和 \(V_{max}\) 值。
Lineweaver-Burk plot
固定抑制剂浓度,以 \(\frac{1}{v}\) 对 \(\frac{1}{[S]}\) 作图,连接得到一条直线,称为 Lineweaver-Burk plot;有几个抑制剂浓度,就可以得到几条直线。
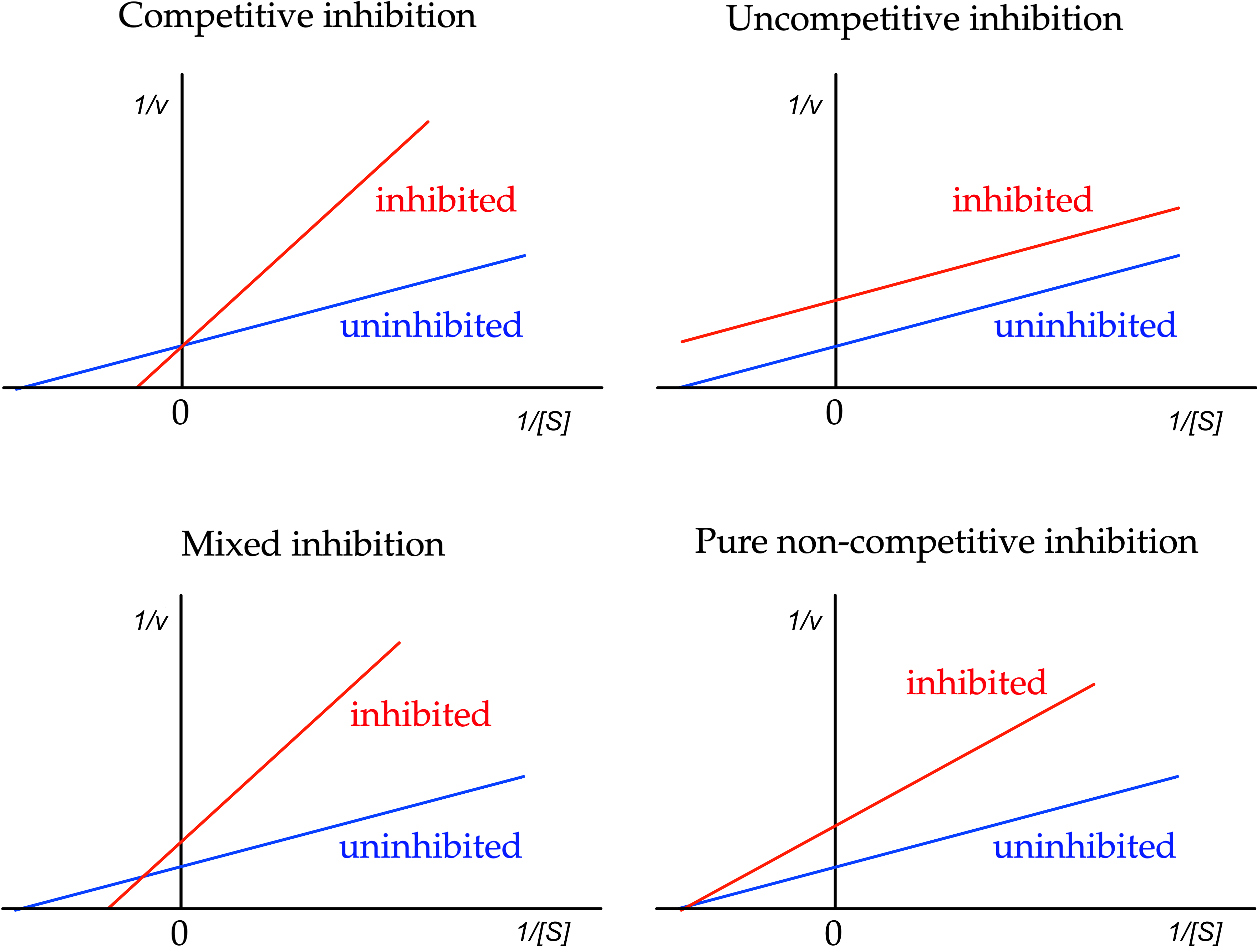
Figure 3. Lineweaver-Burk plot
| 抑制类型 | 图形特征 |
|---|---|
| 竞争性抑制 | 所有直线相交于 \(x\) 轴上同一点 |
| 反竞争性抑制 | 所有直线互相平行 |
| 混合型抑制 | 所有直线相交于 \(x\) 轴负半轴和 \(y\) 轴构成的第二象限内 |
| 非竞争性抑制 | 所有直线相交于 \(x\) 轴的负半轴上某一点 |
Dixon plot
固定底物浓度,以初始速率的倒数 \(\frac{1}{v}\) 对抑制剂浓度 \([I]\) 作图,连接得到一条直线,称为 Dixon plot。有几个固定底物浓度,就可以得到几条直线。
| 抑制类型 | 图形特征 | \(K_{i}\) |
|---|---|---|
| 竞争性抑制 | 所有直线相交于第二象限 | 交点的横坐标的相反数 |
| 非竞争性抑制 | 所有直线相交于 \(x\) 轴的负半轴上 | 交点的横坐标的相反数 |
| 反竞争性抑制 | 所有直线平行 | / |
| 混合型抑制 | 所有直线相交于第二象限 | 交点的横坐标的相反数 |
Secondary plot
以 Lineweaver-Burk 图中得到的斜率(Sloop)对抑制剂浓度 \([I]\) 作图,连接得到一条直线,称为二级重绘图(Secondary plot)。
- x 轴截距即为 \(-K_{i}\)。
- y 轴截距是在没有抑制剂(\([I]=0\))时,Lineweaver-Burk 图的斜率,即 \(\frac{K_m}{V_{max}}\)。
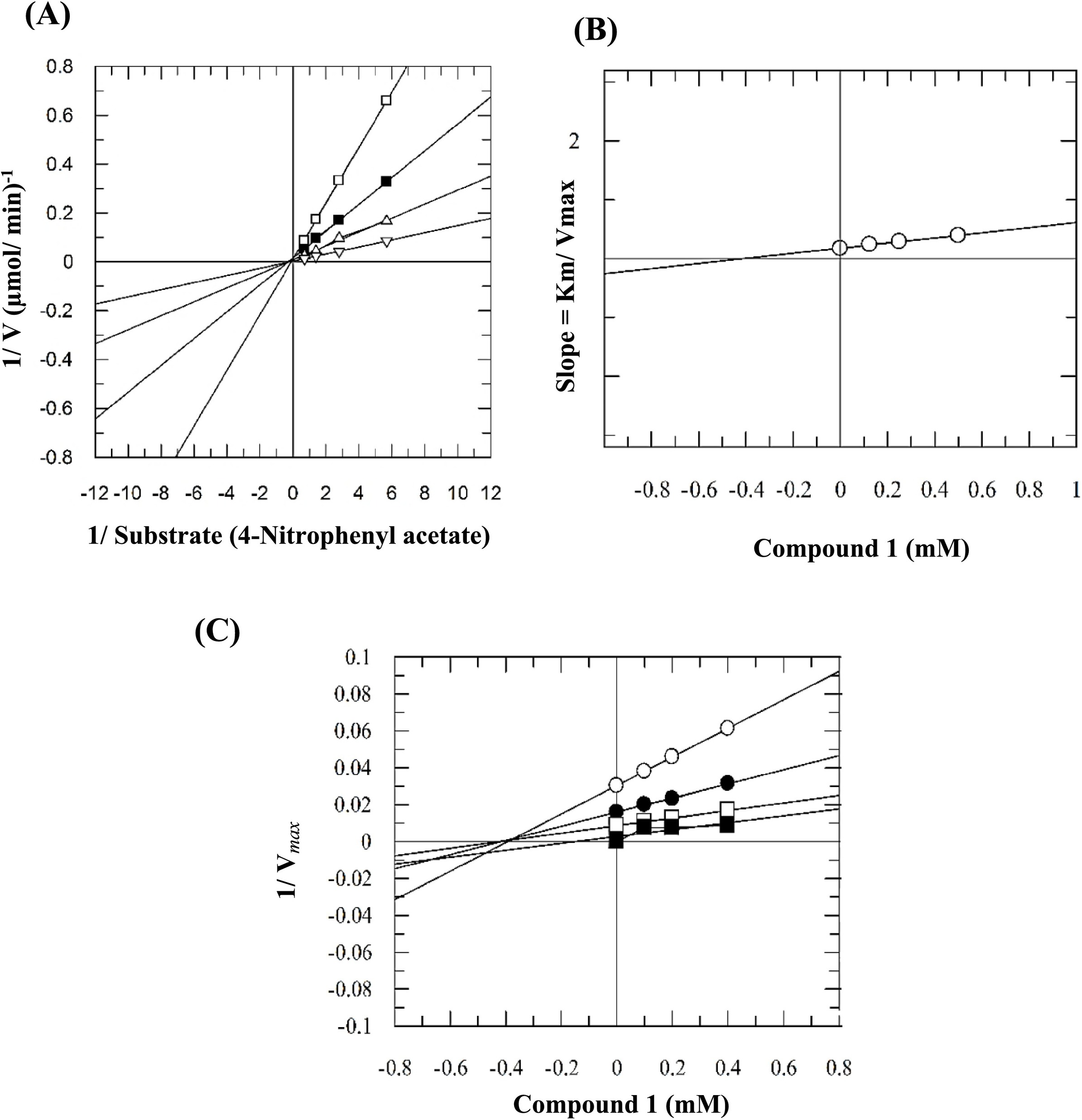
Figure 4. 抑制常数测量示例:(A) Lineweaver-Burk plot, (B) Secondary plot, and (C) Dixon plot
附:Cheng-Prusoff 方程
Cheng-Prusoff 方程可以将 \(IC_{50}\) 值转换成绝对抑制常数 \(K_{i}\),使不同底物浓度下测量的 \(IC_{50}\) 具有可比性。
| 抑制类型 | \(IC_{50}\) 与 \(K_i\) 的关系 | \(IC_{50}\) 如何随 \([S]\) 变化 |
|---|---|---|
| 竞争性抑制 | \(K_i = \frac{IC_{50}}{1 + \frac{[S]}{K_{m}}}\) | 增大 |
| 非竞争性抑制 | \(K_i = IC_{50}\) | 不变 |
| 反竞争性抑制 | \(K_i = \frac{IC_{50}}{1 + \frac{K_{m}}{[S]}}\) | 减小 |
| 混合型抑制 | \(IC_{50}=\frac{K_m+[S]}{\frac{K_m}{K_i}+\frac{[S]}{K_i^{\prime}}}\) | 增大或减小 |
注:对混合型抑制,设 \(K_i^{\prime}=\alpha\cdot K_i\),有 \(IC_{50}=\frac{K_m+[S]}{\frac{K_m}{K_i}+\frac{[S]}{\alpha K_i}}=K_i\cdot\frac{\alpha(K_m+[S])}{\alpha K_m+[S]}\)。
Cheng-Prusoff 方程也可用于计算 \(K_{i}\)。在已知动力学参数(\(K_{m}\))及抑制剂抑制类型下,可以用 \(IC_{50}\) 及对应的 \([S]\) 计算 \(K_{i}\)。
半数抑制浓度
半数抑制浓度(\(IC_{50}\)) 指抑制 50% 给定生物过程或生物成分时抑制剂的浓度。
对抑制率 % 有:
\[ \text{\% } \text{Inhibition} = \frac{[I]^{n}}{K_{i}^{n}[I]^{n}} \]
以抑制剂浓度 \([I]\) 对 \(\text{\% } \text{Inhibition}\) 作图,曲线呈 S 形。\(IC_{50}\) 指 \(\text{\% } \text{Inhibition} = 50\%\) 时的 \([I]\)。
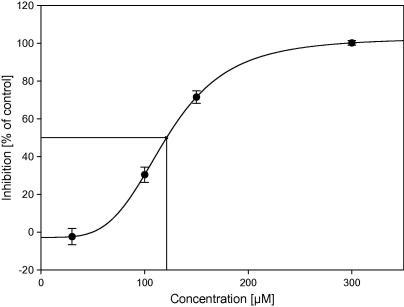
Figure 5. 浓度和抑制率 % 曲线
\(IC_{50}\) 的测量
以酶活实验为例,在固定的酶浓度和底物浓度(通常在 \(K_{m}\) 值附近,此时反应最敏感)下,通过测量一系列不同抑制剂浓度 \([I]\) 及对应的 \(\text{\% } \text{Inhibition}\),然后进行拟合求解。
References
高国全, 汤其群. 生物化学与分子生物学 [M]. 第10 版. 北京:人民卫生出版社, 2024.
Google Gemini with 2.5 Pro
By Athel cb - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=130486959 (Figure 3)
Identification, crystallization, and first X-ray structure analyses of phenyl boronic acid-based inhibitors of human carbonic anhydrase-II: https://doi.org/10.1016/j.ijbiomac.2024.131268 (Figure 4)
By Blunder M, Hurkes N, Spirk S, List M, Pietschnig R - Bioorganic & medicinal chemistry letters (2010) - https://openi.nlm.nih.gov/detailedresult?img=PMC3013380_gr2&req=4, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=138731109 (Figure 5)