新药研发中的专利保护
专利
什么是专利
专利是对发明授予的一种专有权利。换言之,专利是对产品或方法的专有权利,这种产品或方法提供了新的做事方式或对某一问题提出新的技术解决方案。要取得专利,必须在一份专利申请中向公众披露发明的技术信息。1
即申请人通过向社会公开发明,以换取权利机关授予申请人在一定期限内享有专有权利。
专利是对发明授予的一种专有权利。换言之,专利是对产品或方法的专有权利,这种产品或方法提供了新的做事方式或对某一问题提出新的技术解决方案。要取得专利,必须在一份专利申请中向公众披露发明的技术信息。1
即申请人通过向社会公开发明,以换取权利机关授予申请人在一定期限内享有专有权利。
我们先来理解一下液相系统流路:
\[ \text{泵/混合器} \xrightarrow{t_A} \text{进样器} \xrightarrow{t_B} \text{色谱柱} \xrightarrow{t_C} \text{检测器} \]
在色谱图上,\(t = 0\) min 是指样品从进样器注入到流路的瞬间。
graph LR 1-1[有关样品的情况,明确分离目的] --> 2-1[是否需要特殊的 HPLC 步骤、样品预处理等?] --> 3-1[选择检测器和检测器设备] --> 4-1[选择液相色谱法,进行预试验,估计最佳分离条件] --> 5-1[优化分离条件] --> 6-1[检查出现的问题或所需的特殊步骤] --> 7-1[论证方法使之进入常规实验室]
一个好的分析方法,应该尽量满足:
色谱流出曲线(elution profile):经色谱柱分离后的各组分随流动相依次进入检测器,检测器将流动相中各组分浓度或质量的变化转变为可测量的电信号,记录此信号强度随时间变化的曲线,称为色谱流出曲线,又称为色谱图(chromatogram)。
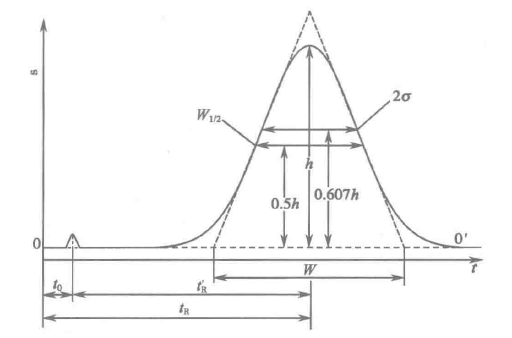
Figure 1. 色谱流出曲线
我们知道理想色谱峰是对称。但如果具体去了解相关内容,通常会告诉我们理想的色谱峰不仅是对称的,更是近似于正态分布曲线。以人民卫生出版社《分析化学》第 8 版为例:
正常色谱峰为对称形正态分布曲线,曲线有最高点,以此点的横坐标为中心,曲线对称地向两侧快速、单调下降。
那么,该如何理解“理想的色谱峰近似于正态分布曲线”呢?
首先我们假设没有色谱柱的存在。当我们足够快地向流路中注入化合物,化合物被迅速洗脱,并被检测器检测到。因为我们注入速度和洗脱速度足够快,色谱峰是一条 \(t=0\) 竖线。
1902 年 Victor Henri 提出了酶- 底物中间复合物学说,认为首先是酶 E 与底物 S 生成酶-底物 中间复合物 ES,然后 ES 分解生成产物 P 和游离的酶。
\[ \ce{E + S <=>[k_1][k_2] ES ->[k_3] E + P} \]
式中的 \(k_{1}\)、\(k_{2}\) 和 \(k_{3}\) 分别为各向反应的速率常数。
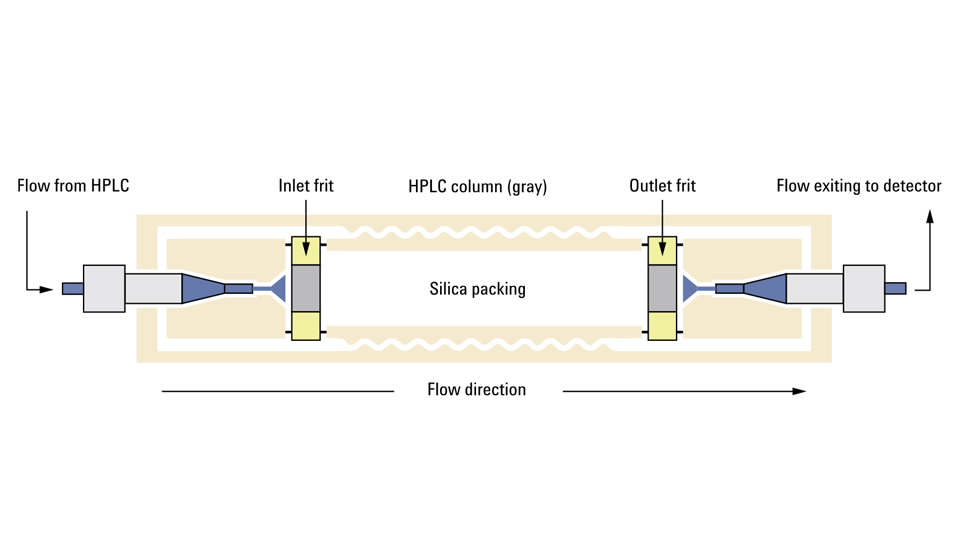
Figure 1. 液相色谱柱
常见的 HPLC 色谱柱由不锈钢柱体和两端的筛板(frit),以及柱内填料组成。两端的筛板主要防止填充颗粒流失和色谱柱堵塞;对于分配色谱,填料通常以硅胶颗粒作为载体,在硅胶表面键合有固定相。
2025.05.11
基于目前个人对统计学的理解,做了一个假设检验方法选择的思维导图。目前仅是从采集的数据类型切入的,对于假设检验方法的选择应该还是比较直观易懂。
如果是从自变量和因变量角度来看,如单因素方差分析,可以看作分类数据自变量对定量数据因变量的影响,因此也就能将“回归相关”纳入到一个更大体系里。后面可能也出一版这样的思维导图。
统计学是关于数据资料的收集、整理、分析和推断的一门科学。它可分为描述统计学和推断统计学两大类。
描述统计学是研究数据收集、处理、描述及可视化的统计学方法,其内容包括如何取得研究所需要的数据,如何用图表形式对数据进行处理和展示,如何通过对数据的综合、概括与分析,得出所关心的数据特征。如果在研究中可以得到整个总体的数据,那么描述统计学就足够了。
但是,实际中往往只能得到总体的一小部分(称为样本),这就需要通过这些样本的有限的样本信息来推断有关总体特征,这就是推断统计学的研究领域,又分为参数估计和假设检验。
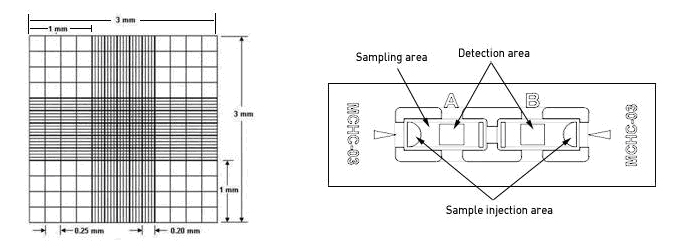
血球计数板用优质厚玻璃制成,通过 H 形凹槽分为两个相同的计数池。每个计数池的两侧都有一个支持柱,上面覆盖着特制的盖玻片,形成高度为 0.10 mm 的计数池。
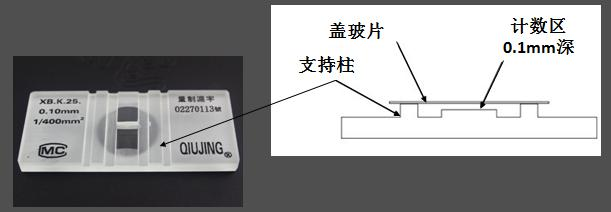
计数池内划分为长和宽各为 3 mm 的方格,总共分为 9 个大方格。每个大格面积为 1.0 mm,体积为 0.1 mm3,即一个大方格的体积是 0.1 μL。