高效液相色谱方法的建立 00:基础概念
基本概念
色谱流出曲线
色谱流出曲线(elution profile):经色谱柱分离后的各组分随流动相依次进入检测器,检测器将流动相中各组分浓度或质量的变化转变为可测量的电信号,记录此信号强度随时间变化的曲线,称为色谱流出曲线,又称为色谱图(chromatogram)。
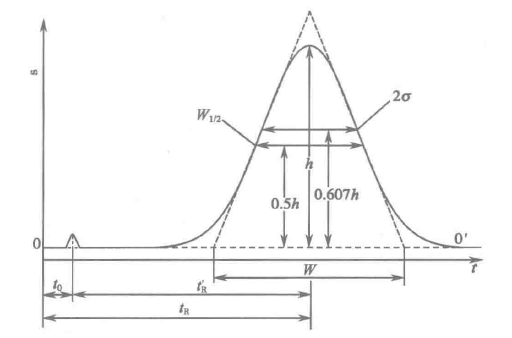
Figure 1. 色谱流出曲线
基线(base line) :仅有流动相通过检测器时,所得到的流出曲线称为基线。稳定的基线是一条平行于横轴(时间轴)的直线。
色谱峰(peak) :色谱流出曲线上的突起部分称为色谱峰。理想的色谱峰近似于正态分布曲线(高斯分布曲线)。异常峰有两种:拖尾峰(tailing peak)和前延峰(leading peak)。拖尾峰是前沿陡峭、后沿平缓;前延峰是前沿平缓、后沿陡峭。
峰高(peak height, \(h\)) :色谱峰顶点与基线之间的垂直距离。
标准差 (standard deviation, \(σ\)): 正态色谱流出曲线上两拐点间距离之半称为标准差。标准差是可用来衡量组分被洗脱出色谱柱的分散程度的参数,其值越大,组分越分散;反之越集中。对于正态峰,σ 等于高点 0.607 倍处峰宽的一半。
半峰宽(peak width at half height, \(W_{1/2}\))峰高一半处的峰宽称为半峰宽。正态色谱峰半峰宽与标准差的关系为:
\[ W_{1/2} = 2.355\sigma \]
- 峰宽(peak width, \(W\)):通过色谱峰两侧拐点作切线,在基线上所截得的距离称为峰宽,也称为基线宽度。正态色谱峰峰宽与标准差或半峰宽的关系为:
\[ W = 4\sigma \quad \text{或} \quad W = 1.699W_{1/2} \]
- 峰面积(peak area, \(A\)):色谱峰曲线与基线间包围的面积称为峰面积。正态色谱峰的峰面积与峰高和半峰宽的关系为:
\[ A = 1.065h \cdot W_{1/2} \]
色谱参数
相平衡参数
色谱过程是样品组分在固定相和流动相之间反复多次的“分配”过程,这种“分配”过程常用分配系数和容量因子来描述。
- 分配系数(partition coefficient, \(K\)):在一定温度和压力下,组分在两相中达到分配平衡后,其在固定相与流动相中的浓度之比称为分配系数,即
\[ K = \frac{c_s}{c_m} \]
式中,\(c_s\) 和 \(c_m\) 分别为组分在固定相和流动相中的浓度。 分配系数仅与组分、固定相和流动相的性质及温度有关。 在一定条件(固定相、流动相、温度)下,分配系数是组分的特征常数。
上式是对液-液分配色谱法分配系数的定义,即狭义分配系数。广义分配系数包括:分配色谱法的分配系数、吸附色谱法的吸附系数、离子交换色谱法的选择性系数及凝胶色谱法中的渗透系数。这些分配系数的物理意义虽然各异,但都可用上式来表示。
- 容量因子(capacity factor, \(k\)):也称保留因子(fetention factor, \(k\)),在一定温度和压力下,组分在两相中达到分配平衡后,其在固定相和流动相中的质量之比称为容量因子,又称为质量分配系数或分配比,即
\[ k = \frac{m_s}{m_m} = \frac{c_sV_s}{c_mV_m} = K\frac{V_s}{V_m}=\frac{t_R-t_0}{t_0} \]
- 分离因子(separation factor, \(\alpha\)):也称选择因子(selectivity factor, \(\alpha\)),定义为后一组分与前一组分容量因子之比,即:
\[ \alpha = \frac{k_{2}}{k_{1}} \]
保留参数
保留时间(retention time, \(t_R\)) :从进样到某组分在柱后出现浓度极大时的时间间隔,即从进样开始到某组分的色谱峰顶点的时间间隔。保留时间是色谱法的基本定性参数。
死时间(dead time, \(t_0\)) :不被固定相保留的组分从进样到其在柱后出现浓度极大时的时间间隔,称为死时间。死时间可以通过以下方式估算:
- 第一个显著的基线波动;
- 用极强的溶剂作为流动相;
- 通过柱尺寸计算;
- 注入不保留的样品,尿嘧啶、丙酮和硫脲是反相色谱中最常用的测试物质。
调整保留时间(adjusted retention time, \(t_{R}^{\prime}\)) :某组分由于与固定相发生作用而被固定相保留,比不被固定相保留的组分在色谱柱中多停留的时间称为调整保留时间,即组分在固定相中滞留的时间。调整保留时间与保留时间和死时间的关系为:
\[ t^{\prime}_R = t_R - t_0 \]
在实验条件(温度、固定相等)一定时,调整保留时间仅决定于组分的性质,因此它是常用的色谱定性参数之一。
- 保留体积(retention volume, \(V_{R}\)) :从进样开始到某组分在柱后出现浓度极大时所需通过色谱柱的流动相体积。保留体积与保留时间和流动相流速(\(F_c\), mL/min)的关系为:
\[ V_{R}=t_{R}\cdot F_{c} \]
流动相流速大,组分的保留时间短,但两者的乘积不变,因此保留体积与流动相流速无关。
- 死体积(dead volume, \(V_{0}\)):由进样器至检测器的流路中未被固定相占有的空间体积称为死体积。 死体积是色谱柱中从进样器至色谱柱间导管的容积、固定相的孔隙及颗粒间隙、柱出口导管及检测器内腔容积的总和。 如果忽略各种柱外死体积,则死体积近似为流动相在色谱柱中占有的体积,而死时间则相当于流动相充满死体积所需的时间。 死体积与死时间和流动相流速的关系为:
\[ V_{0}=t_{0}\cdot F_{c} \]
- 调整保留体积(adjusted retention volume, \(V_{R}\)′):由保留体积扣除死体积后的体积称为调整保留体积,调整保留体积与保留体积和死体积的关系为:
\[ V^{\prime}_{R} = V_{R} - V_{0} = t^{\prime}_{R} \cdot F_{c} \]
调整保留体积与流动相流速无关,是常用的色谱定性参数之一。
- 保留指数(retention index, \(RI\)):把组分的保留行为换算成相当于含有几个碳的正构烷烃的保留行为,通常是用与被测组分的保留时间相近的两个正构烷烃作为标准,来标定被测组分的保留指数。
在恒温条件下,化合物的保留行为遵循对数关系,有:
\[ RI=100\times\left[n+\frac{\log(t_{Rx}^{\prime})-\log(t_{Rn}^{\prime})}{\log(t_{R(n+1)}^{\prime})-\log(t_{Rn}^{\prime})}\right] \]
- \(t^{\prime}_{Rx}\):待测物 \(x\) 的调整保留时间;
- \(t^{\prime}_{Rn}\):紧邻待测物 \(x\) 之前出峰的正构烷烃的调整保留时间;
- \(t^{\prime}_{R(n+1)}\):紧邻待测物 \(x\) 之后出峰的正构烷烃的调整保留时间;
- \(n\):前一个正构烷烃的碳原子数。
在程序升温条件下,化合物的保留时间与碳数近似成线性关系,有:
\[ RI=100\times\left[n+\frac{t_{Rx}-t_{Rn}}{t_{R(n+1)}-t_{Rn}}\right] \]
- \(t_{Rx}\):待测物 \(x\) 的绝对保留时间;
- \(t_{Rn}\):紧邻待测物 \(x\) 之前出峰的正构烷烃的调整保留时间;
- \(t_{R(n+1)}\):紧邻待测物 \(x\) 之后出峰的正构烷烃的调整保留时间;
- \(n\):前一个正构烷烃的碳原子数。
分离度
- 分离度(resolution, \(R_{s}\)):是描述相邻两组分在色谱柱中分离情况的参数,其定义式为:
\[ R_{s} = \frac{2(t_{R2} - t_{R1})}{W_1 + W_2} \]
实际使用中,常用半峰宽来计算:
\[ R_{s} = \frac{1.18(t_{R2} - t_{R1})}{W_{1/2,1} + W_{1/2,2}} \]
要使两组分有足够的分离度,一方面是两组分的保留时间要有较大的差异;另一方面色谱峰宽要足够窄。
色谱理论
塔板理论
塔板理论将色谱柱看作一个分馏塔,并假定在色谱柱中存在一系列理论塔板,每个塔板内组分在固定相和流动相之间达到分配平衡。理论塔板数越多,柱效率越高,分离能力越强。
塔板理论是在如下基本假设的前提下提出的:
- 在色谱柱内一下段高度 \(H\) 内,组分可以在两相中瞬间达到动态分配平衡,\(H\) 称为塔板高度;
- 分配系数在各塔板内是常数;
- 流动相不是连续地而是间歇式地进入色谱柱,且每次只能进入一个塔板体积;
- 样品组分都是先加在第 0 号塔板上,且组分的纵向扩散可以忽略不计。
理论塔板数(number of theoretical plates):
\[ n = \left( \frac{t_R}{\sigma} \right)^2 = 16 \left( \frac{t_R}{W} \right)^2 = 5.54 \left( \frac{t_R}{W_{1/2}} \right)^2 \]
理论塔板高度(height of equivalent to a theoretical plate)
\[H=\frac{L}{n}\]
为什么理想的色谱峰近似于正态分布曲线?
设容量因子 \(k=\frac{m_s}{m_m}=\frac{q}{p}\),且 \(p+q=1\),其中 \(p\) 可以理解为 1 个化合物分子完成一次分配后,存在于流动相中而不被固定相截留(保留)的概率。
当 1 个化合物分子,经过 \(n\) 个塔板分配后,假设其中有 \(r\) 次没有被固定相截留,其发生概率满足二项分布:
\[P(X=r)=C_{n}^{r}\cdot p^{r}\cdot (1-p)^{n-r}\]
\(P(X=r)\) 表示在 \(n\) 次独立重复的伯努利试验(只有两种可能结果的单次随机试验)中,所期望的事件恰好发生 \(r\) 次的概率。
当 1 个化合物分子在 \(n\) 次分配中,有 \(r\) 次通过塔板,最终就会存在于第 \(r\) 号的塔板内。因此,当有大量的分子时同时注入色谱柱时,化合物在空间分布上的分布也近似于二项分布概率密度函数。
当 \(p\neq0.5\) 时,二项分布概率密度函数是偏倚的,随着 \(n\) 值增大,分布逐渐趋于对称。棣莫弗-拉普拉斯定理(De Moivre–Laplace theorem)指出,当 \(n\to\infty\) 时,二项分布趋近于正态分布。
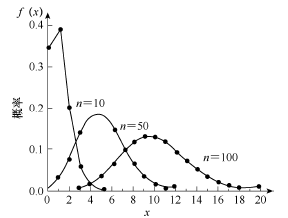
Figure 2. \(n\) 值不同的二项分布
因此,当塔板数足够大(如 \(n>2000\))时,色谱峰近似于正态分布曲线。
速率理论
色谱峰的展宽是由于组分分子在色谱柱内无规则运动的结果,这种随机过程导致组分分子在色谱柱内呈正态分布,因此标准差 \(\sigma\) 或方差 \(\sigma^2\) 作为组分分子在色谱柱内离散程度的量度,总的离散程度 \(\sigma^2\) 是单位柱长内分子离散的累积,且与柱长成正比,即
\[\sigma^2=HL\]
式中:\(H\) 为比例系数;\(\sigma^2\) 为随机变量的分散程度,则 \(H\) 为单位柱长的分子离散,即
\[H=\frac{\sigma^2}{L}\]
\(H\) 仍称为塔板高度,但与塔板理论中的塔板高度具有不同的含义。速率理论的塔板高度是柱内单位长度中组分分子离散的程度,作为一个色谱参数使用,是描述色谱峰展宽的指标。
速率理论方程
van Deemter 根据气相色谱过程中的物料平衡、扩散及传质现象与组分运动速率的关系的偏微分方程,导出了速率理论方程,又称 van Deemter 方程:
\[ H = A + \frac{B}{u} + Cu \]
- \(H\):塔板高度(cm);
- \(A\):涡流扩散系数(cm);
- \(B\):纵向扩散系数(cm2/s);
- \(C\):传质阻抗系数(s);
- \(u\):流动相的线速度(cm/s),\(u=\frac{L}{t_{0}}\)。
涡流扩散
涡流扩散(eddy diffusion):涡流扩散也称为多径扩散。指由于填充不均匀,使同一组分的不同分子经过多个不同长度的途径流出色谱柱,造成色谱峰展宽。
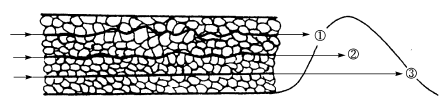
Figure 3. 涡流扩散对色谱峰展宽的影响
纵向扩散
纵向扩散(longitudinal diffusion):纵向扩散也称分子扩散,组分进入色谱柱时,是以“塞子”的形式存在于色谱柱的很小的一段空间中,由于浓度梯度的存在,组分将向“塞子”前、后扩散,造成色谱法展宽。
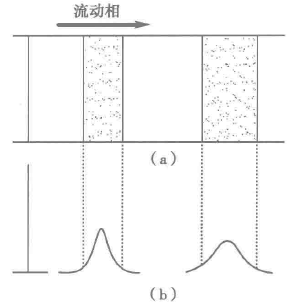
Figure 4. 纵向扩散产生的峰展宽,(a)柱内谱带,(b)相应的色谱峰
传质阻抗
传质阻抗(mass transfer resistance),组分被流动相带入色谱柱后,通过两相界面进入固定相,并扩散至固定相内部,进而达到动态平衡。当纯的或含有低于平衡浓度的流动相到来时,固定相中组分的部分分子将回到两相界面,移除,而后被流动相带走。这种溶解、扩散、转移的过程称为传质过程。影响此过程进行的阻力称为传质阻抗。由于传质阻抗的存在,组分不能在两相间瞬间达到平衡,即色谱柱总是在非平衡状态下工作,结果是有些分子随流动相向前移动较快(与平衡状态下的分子比较),而另一些分子则滞后,从而引起峰展宽。
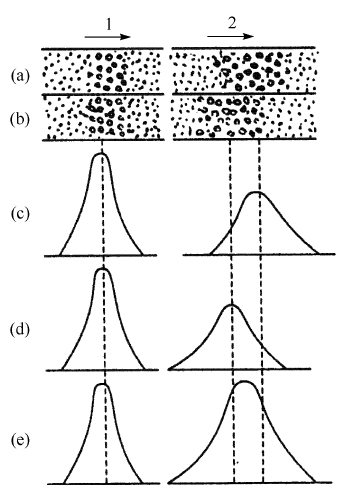
Figure 5. 传质阻力对色谱峰展宽的影响:(a)流动相;(b)固定相;(c)流动相中组分的分布;(d)固定相中组分的分布;(e)色谱峰形状
流速对柱效的影响
由 van Deemter 方程可知,涡流扩散项(\(A\))不随流速变化,纵向扩散项(\(\frac{B}{u}\))随流速增加而减小,传质阻抗项(\(C\cdot u\))随流速增加而增加。塔板高度(\(H\))随流速(\(u\))先下降后上升,且有一最有流速(\(u_{opt}\))使塔板高度最小,即 \(H_{min}\)。
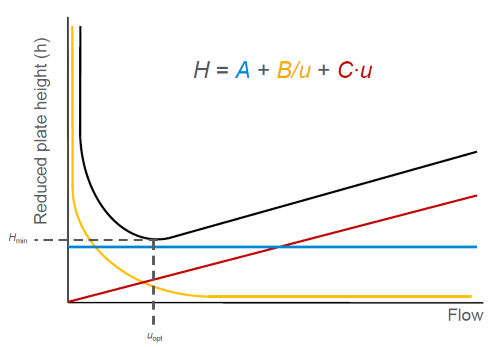
Figure 6. 流速对塔板高度的影响
References
柴逸峰, 邸欣. 分析化学[M]. 8版. 北京: 人民卫生出版社, 2016.
李春喜, 姜丽娜, 邵云, 等. 生物统计学[M]. 6版. 北京: 科学出版社, 2023.
HPLC Method Development- From Beginner to Expert, Part 1: https://www.agilent.com/cs/library/slidepresentation/public/method-development-101-from-beginner-to-expert-part-1-feb202024.pdf