质谱基础知识 04:详解四极杆原理
前言
在《质谱基础知识 03:质量分析器》中简单介绍了四极杆原理,这里再进行一些补充。此外限于个人能力,没能对离子运动的 Mathieu 方程进行推导,如有需要可以参阅《质谱分析技术原理与应用》相关章节。
四极杆结构
四极杆质量分析器,由四个平行的双曲面杆状电极组成,以两个电极为一组,分为 \(x\) 与 \(y\) 两组电极平行并对称于一中心轴排列。
每组电极由以下两种电压叠加组成:
- 射频(Radio Frequency, RF)电压:20 kHz 到 300 GHz 的高频交流电,用 \(V \cos \omega t\) 表示;
- 直流(DC)电压:用 \(U\) 表示,由于该电压在四极杆中用于选择离子,也被称为过滤直流电压(Filtering DC, FDC);
其中一组电极为 \(U + V \cos \omega t\);另一组电极相位与其相差 180°,表示为 \(-(U + V \cos \omega t)\)。
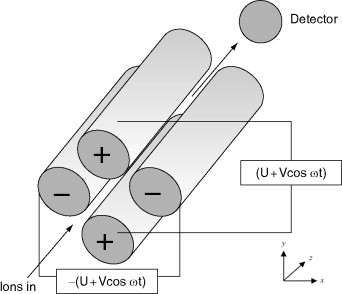
Figure 1. 四极杆示意图
- \(U\):直流电压(DC)
- \(V\):射频电压振幅(RF)
- \(\omega\):射频角频率
- \(t\):时间
此外,一些厂家的四极杆在 \(z\) 轴方向还施加一较低的直流电压,为离子提供轴向飞行的能量,该电压称为轴向补偿电压(Rod Offset Voltage, ROF)。
Mathieu 方程
Mathieu 方程是描述四极杆中离子运动的数学基础,其标准形式为
\[ \frac{d^2u}{d\xi^2}+\left(a-2q\cos2\xi\right)u=0 \]
Mathieu 方程的解受到参数 \((q, a)\) 控制,当 \((q, a)\) 位于稳定区时,方程的解 \((u, \xi)\) 是有界的;当 \((q, a)\) 位于不稳定区时,方程的解 \((u, \xi)\) 是无界的。
如果用 Mathieu 方程来描述一个系统的运动(位移 \(x\) 随时间 \(t\) 的变化),当参数 \((q, a)\) 位于稳定区时(Figure 2 中阴影部分),系统运动始终有界——无论过多久,位移都不会超过某个有限范围;当 \((q, a)\) 位于不稳定区时,系统通常会指数发散——随着时间推移,振荡幅度越来越大,最终趋于无穷。
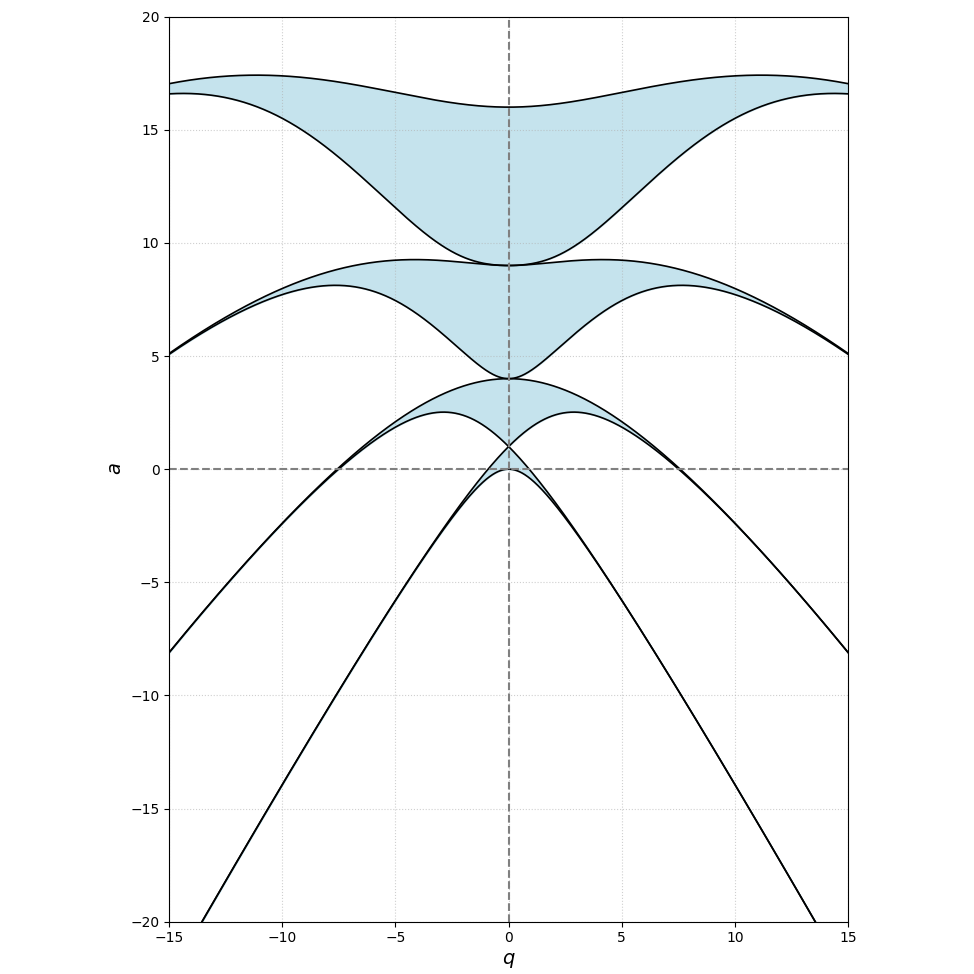
Figure 2. Mathieu 方程稳定图(图中蓝色阴影部分为稳定区)
对于理想的双曲线四极杆电极,四极杆中离子在 \(x\) 轴和 \(y\) 轴的运动可以分别整理成标准的 Mathieu 方程:
\[ \frac{\mathrm{d}^{2}x}{\mathrm{d}t^{2}} + \frac{2ze}{mr_{0}^{2}}\left(U + V\cos\omega t\right)x = 0 \]
\[ \frac{\mathrm{d}^{2}y}{\mathrm{d}t^{2}} - \frac{2ze}{mr_{0}^{2}}\left(U + V\cos\omega t\right)y = 0 \] 其中,
\[ q=q_{x}=-q_{y}=\frac{4zeV}{mr_{0}^{2}\omega^{2}} \]
\[ a=a_{x}=-a_{y}=\frac{8zeU}{mr_{0}^{2}\omega^{2}} \]
\[ \xi = \frac{\omega t}{2} \]
- \(e\):离子电荷(C)
- \(m\):离子质量(kg)
- \(r_0\):四极杆半径(从中心轴到电极表面的距离,m)
- \(U\):直流电压(V)
- \(V\):射频电压振幅(V)
- \(ω=2πf\):射频角频率(rad/s)
在 \(x\) 轴方向,当对于给定电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) ,当其位于 Figure 2 中稳定区时,离子在四极杆中的 \(x\) 方向是有界的。
在 \(y\) 轴方向,当对于给定电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) ,由于
\[ q=q_{x}=-q_{y}=\frac{4zeV}{mr_{0}^{2}\omega^{2}} \]
\[ a=a_{x}=-a_{y}=\frac{8zeU}{mr_{0}^{2}\omega^{2}} \]
其稳定图与 \(x\) 轴的稳定图关于坐标原点中心对称,如 Figure 3 所示。
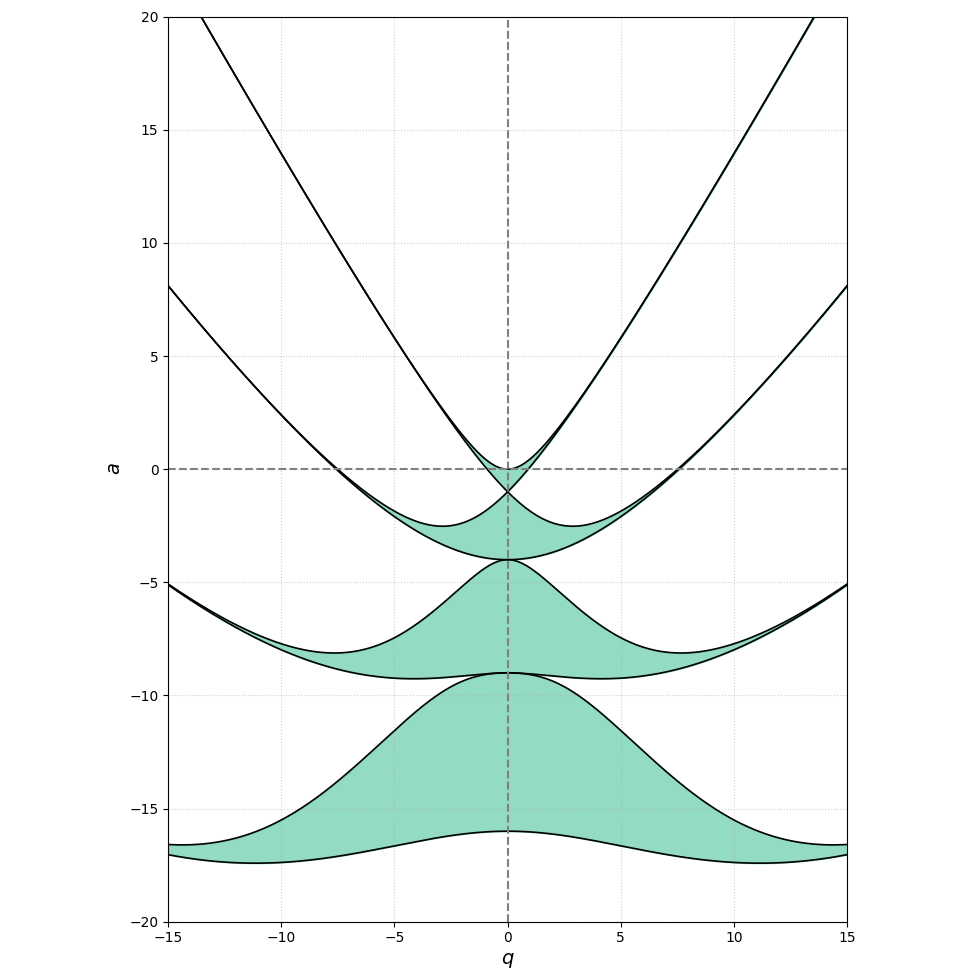
Figure 3. 对于给定电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) 时,\(y\) 轴的稳定图
将 Figure 2 和 Figure 3 合并在同一坐标系上,蓝色阴影和绿色阴影重叠的部分(红色阴影),表示当给定电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) 时位于此区域时,四极杆中的离子在 \(x, y\) 轴上都是有界的;而当电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) 不在此区域时,离子运动轨迹最终会发散,撞上四极杆被中和。
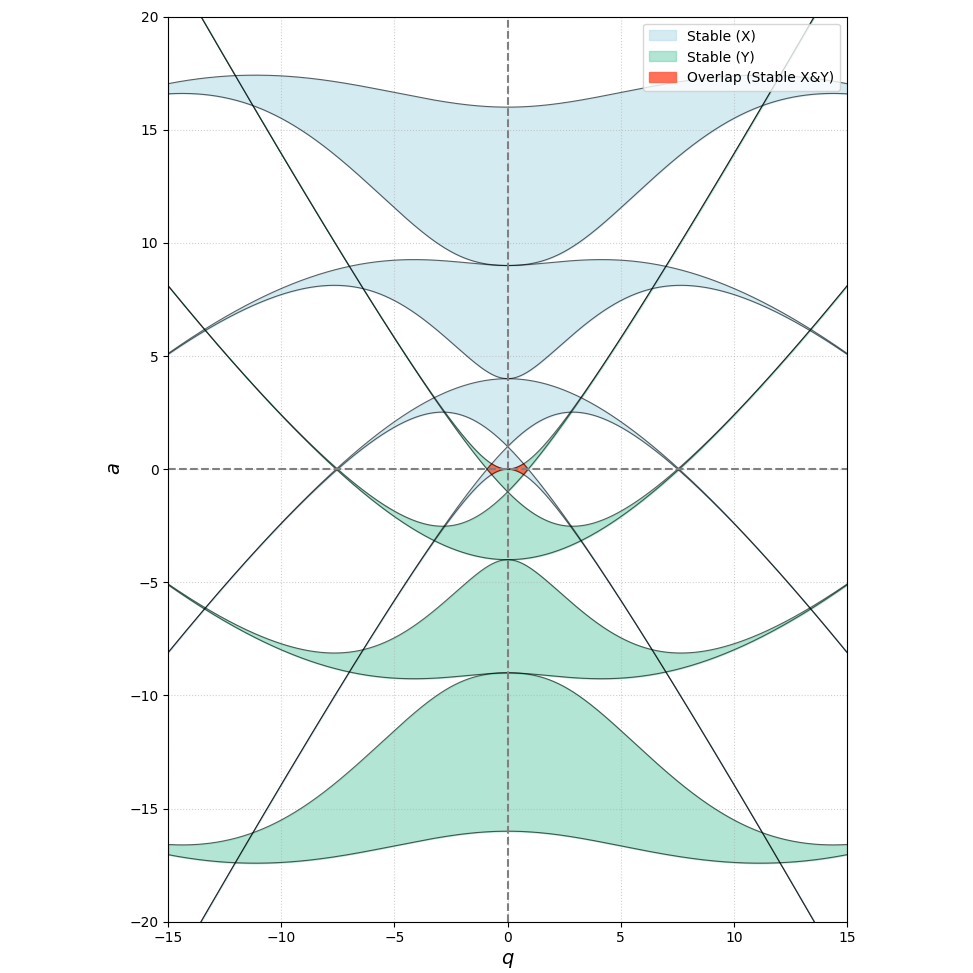
Figure 4. 四极杆中离子稳定图
从 Figure 4 中可以看出,除了坐标原点附近的 \(x, y\) 轴稳定区外,还有多个较小的 \(x, y\) 轴稳定区,但这些稳定区对电压控制要求很高,同时考虑到尽可能使用较小的电压,四极杆中通常只利用坐标原点附近的第一稳定区。
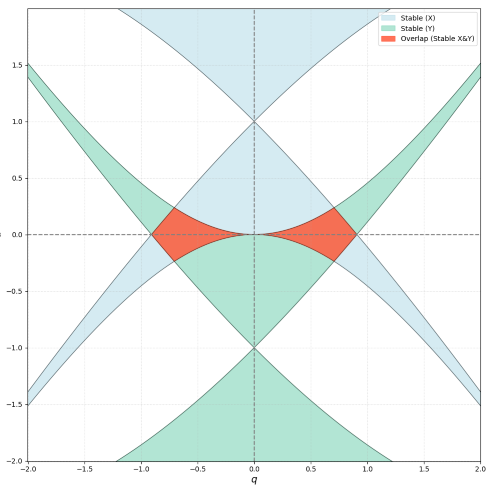
Figure 5. 第一稳定区(红色阴影)
在第一象限,第一稳定区是由 \(a = 0\) 和另外两条曲线围成的类似三角形区域构成。电压参数 \((\frac{4zeV_0}{mr_{0}^{2}\omega^{2}}, \frac{8zeU_0}{mr_{0}^{2}\omega^{2}})\) 中包含了 \(m/z\) 项,将坐标系改为 \(U-V\) 时,随着 \(m/z\) 的增大,第一稳定区也在增大,如 Figure 6(图中 \(z=1\))。
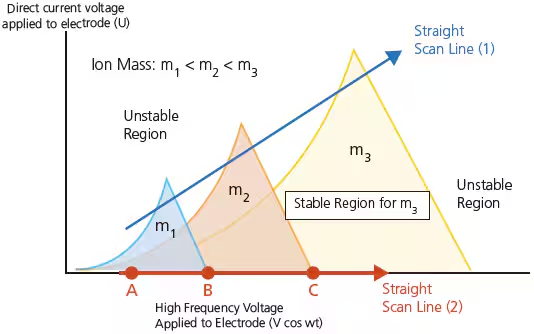
Figure 6. 不同 \(m/z\) 的稳定区
四极杆运行模式
四极杆作为一种离子过滤器,具体是如何实现功能的呢?单个四极杆有三种运行模式:
RF-only(传输模式):将直流电压 \(U\) 设为 0,只施加射频电压 \(V\),如 Figure 6 中 B 点,所有 \(m/z \ge m_1/z_1\) 的离子都位于稳定区,在 \(z\) 轴的初速度或轴向补偿电压(ROF)作用下,都能通过四极杆,起到对大多数离子传输的作用。
SCAN(全扫模式):保持直流电压 \(U\) 和射频电压 \(V\) 的比值(\(U/V\))恒定,同时随着时间线性地增加这两个电压的绝对值,如沿着 Figure 6 中 Scan Line 1 变化,四极杆的“稳定区”会按照时间顺序,依次让从小到大的 \(m/z\) 离子通过。操作线的斜率越接近稳定区尖端,质量选择性越佳,但能通过的离子数量也会变少。检测器记录下离子到达的时间(对应的 \((V, U)\))和强度,最终绘制成质谱图。
SIM(Selected Ion Monitoring,选择离子监控):将 \(U\) 和 \(V\) 固定在特定的数值上,只允许一个(或一组)特定 \(m/z\) 的离子通过,其他离子全部被过滤掉。
References
台湾质谱学会 编著. 质谱分析技术原理与应用[M]. 北京:科学出版社, 2019.
Introduction to mass analyzers : SHIMADZU (Shimadzu Corporation)
Mellon F A. MASS SPECTROMETRY | Principles and Instrumentation[M]//Caballero B. Encyclopedia of Food Sciences and Nutrition (Second Edition). Oxford: Academic Press, 2003: 3739-3749.
河北医科大学药学院液质联用仪(LC-MS)基础应用培训: https://phalab.hebmu.edu.cn/resources/43/202206/1655099489971069569.pdf