统计学笔记 00：如何理解参数估计和假设检验

基础知识

统计学的研究内容

统计学是关于数据资料的收集、整理、分析和推断的一门科学。它可分为描述统计学和推断统计学两大类。

描述统计学是研究数据收集、处理、描述及可视化的统计学方法，其内容包括如何取得研究所需要的数据，如何用图表形式对数据进行处理和展示，如何通过对数据的综合、概括与分析，得出所关心的数据特征。如果在研究中可以得到整个总体的数据，那么描述统计学就足够了。

但是，实际中往往只能得到总体的一小部分（称为样本），这就需要通过这些样本的有限的样本信息来推断有关总体特征，这就是推断统计学的研究领域，又分为参数估计和假设检验。

同质与变异

同质指观察单位或研究个体间具有相同或相近的性质，通常要求主要研究指标的影响因素相同或基本相同。例如，研究一种药物治疗高血压的效果，如果这种药物主要针对原发性高血压的患者，则满足这一条件的患者即为同质观察单位，对于其他如肾病引起的高血压患者则不属于“同质”。

变异是指同一种测量在总体中不同观察单位或个体之间的差别。变异是生物个性的反映，其来源于一些未加控制或无法控制甚至不明原因所致的随机波动。正是因为有“变异”，才需要运用统计学方法对数据进行分析。如果没有变异，所有的研究单位的特征都一样，单一样本就能推断总体特征。

常用描述统计数据的指标

变量是随机变量的简称，变量的观测值称为数据。对于数值型的定量数据，可以从集中趋势和变异程度两个指标方向进行描述。

描述集中趋势的统计学指标

均数是最常用的描述集中趋势的统计学指标之一，其余的指标还有中位数、众数和百分位数等。

均数

\[ \overline{X} = \frac{\sum X}{n} \]

描述变异程度的统计学指标

方差或标准差是最常用的描述集中趋势的统计学指标之一，其余的指标还有极差、四分位数间距和变异系数等。

总体方差

\[ \sigma^{2}=\frac{\sum(X-\mu)^{2}}{n} \]

其中 \(\mu\) 是总体均数。

当直接用样本均数 \(\overline{X}\) 代替总体均数 \(\mu\) 估计方差时，方差会偏大，样本方差的公式校正为

样本方差

\[ S^{2}=\frac{\sum(X-\overline{X})^{2}}{n-1} \]

标准差（Standard Deviation, SD） 是的方差的非负平方根，因此

总体标准差

\[ \sigma=\sqrt{\frac{\sum(X-\mu)^{2}}{n}} \]

样本标准差

\[ S=\sqrt{\frac{\sum(X-\overline{X})^{2}}{n-1}} \]

正态分布

正态分布概率密度函数

将连续型随机变量 \(X\) 与对应出现的可能性 \(f(x)\) 绘制在坐标轴上，就得到了概率密度函数的曲线。而区间 \([a, b]\) 的曲线下面积（图中阴影部分），则表示 \(x\) 取值 \([a, b]\) 的概率，即 \(P(a \leq x \leq b)\).

Figure 1. 连续变量概率密度函数曲线

若连续型随机变量 \(X\) 的概率密度满足

\[ f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad -\infty<x<+\infty \]

其中 \(-\infty<\mu<+\infty,\ \sigma^2>0\)，则称 \(X\) 服从参数为 \(\mu, \sigma\) 的正态分布，记为 \(X\sim N(\mu,\sigma^2)\).

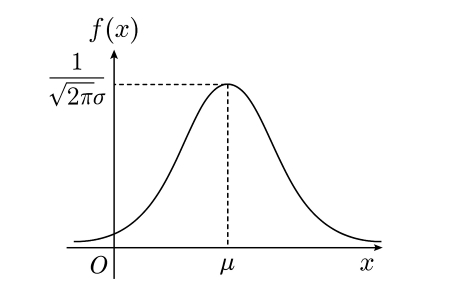
Figure 2. 正态分布概率密度函数曲线

其性质有

• 正态分布的概率密度函数曲线呈钟形，中间高两边低；
• 正态分布的密度函数是以 \(x=\mu\) 为对称轴的对称函数；
• 密度函数在 \(x=\mu\) 处达到最大值

\[ f(\mu)=\frac{1}{\sqrt{2\pi}\sigma} \]

• 在 \((-\infty,\mu)\) 和 \((\mu,+\infty)\) 内严格单调。
• \(\sigma\) 的大小决定了密度函数的陡峭程度，\(σ\) 越大曲线越“矮胖”，表示数据越分散即变异越大，\(σ\) 越小曲线越“瘦高”，表示数据越集中即变异越小。

正态分布曲线下面积

正态分布曲线下的总面积为 \(1\) 或 \(100\%\)，以 \(\mu\) 为中心左右两侧面积各占 \(50\%\)，越靠近 \(\mu\) 处曲线下面积越大，两边逐渐减少。此外还有一些特殊的区间的曲线下面积，可能经常会用到。

范围	面积
\(P(\mu-\sigma \leq x \leq \mu+\sigma)\)	\(68.27\%\)
\(P(\mu-1.96\sigma \leq x \leq \mu+1.96\sigma)\)	\(95.00\%\)
\(P(\mu-2.58\sigma \leq x \leq \mu+2.58\sigma)\)	\(99.00\%\)

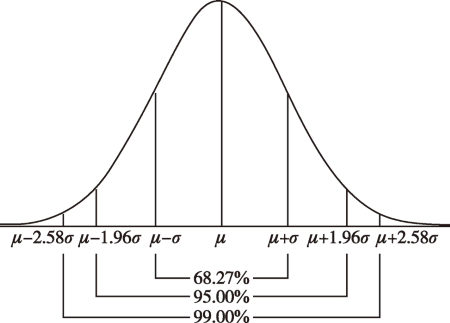
Figure 3. 正态分布曲线下面积

标准正态分布

当正态分布函数 \(\mu=0\), \(\sigma=1\) 时，称 \(X\) 服从标准正态分布，记为 \(X\sim N(0,1^2)\).

对任意 \(X\sim N(\mu,\sigma^2)\)，都有

\[ Z=\frac{X-\mu}{\sigma}\sim N(0,1^2) \] 其中，

\[ Z=\frac{X-\mu}{\sigma} \]

称为随机变量的标准化变换。

抽样

抽样调查是指从总体中抽出部分观察单位组成样本，通过对样本信息的收集和分析，以推断总体的信息特征。与普查相比，抽样调查能以较小的投入获得对总体信息的估计，但为了保证样本的代表性，抽样调查需要按照随机的原则。

抽样误差

由于个体存在变异，因此通过随机抽样得到的样本在推论总体时会存在一定的误差（如样本均数 \(\overline{X}\) 往往不等于总体均数 \(\mu\)），这种由抽样造成的样本统计量与总体参数之间的差异称为抽样误差（sampling error）。

样本均数的分布

理论上（大数定律和中心极限定理）可以证明：若从正态分布总体 \(N(\mu,\sigma^2)\) 中，反复多次随机抽取样本含量固定为 \(n\) 的样本，那么这些样本均数 \(\overline{X}\) 服从参数为 \(\mu, \frac{\sigma}{\sqrt{n}}\) 的正态分布，记为

\[ \overline{X}\sim N(\mu,\frac{\sigma^2}{n}) \]

其中， \(\frac{\sigma}{\sqrt{n}}\) 即样本均数的标准差，称为标准误（Standard error of mean, SEM）：

\[ SEM=\frac{\sigma}{\sqrt{n}} \]

实际中，总体标准差 \(\sigma\) 往往未知，通常用样本标准差 \(S\) 估计 \(\sigma\) ，求得均数标准误的估计值 \(S_{\overline{X}}\)，计算公式为

\[ S_{\overline{X}}=\frac{S}{\sqrt{n}} \]

统计推断

前面提到，现实中往往通过随机抽样调查，通过这些样本的有限的样本信息来推断有关总体特征，这就是推断统计学的研究领域，又分为参数估计和假设检验。

参数估计

参数估计（parameter estimation）指由样本统计量估计总体参数，常有两种方式：

• 点估计：使用单一的数值直接作为总体参数的估计值，如用 \(\overline{X}\) 估计相应的 \(\mu\)，该法表达简单，但未考虑抽样误差的影响，无法评价参数估计的准确程度。
• 区间估计是指按预先给定的概率，计算出一个区间，使它能够包含未知的总体参数。事先给定的概率 \(1−α\) 称为置信度（通常取 \(0.95\) 或 \(0.99\)），计算得到的区间称为置信区间（confidence interval, CI）。置信区间通常由两个数值界定的置信限（confidence limit）构成，其中数值较小的一方称为下限，数值较大的一方称为上限。

总体均数估计的 95% 置信区间表示该区间包括总体均数 \(\mu\) 的概率为 \(95\%\)，即若每作 100 次抽样算得 100 个置信区间，则平均有 95 个置信区间包括 \(\mu\)（估计正确），只有 5 个置信区间不包括 \(\mu\)（估计错误）。

小概率事件：统计学上把小于等于 \(0.05\) 或 \(0.01\) 的概率称为小概率，认为小概率事件在一次试验中看成是几乎不可能发生。

下面以示例来进行置信区间的估计：

某医生测得 \(n\) 名动脉粥样硬化患者血浆纤维蛋白原含量的均数为 \(\overline{X}\) g/mL，标准差为 \(S\) g/mL，试计算该种病人血浆纤维蛋白原含量总体均数的 95% 置信区间。

因为

\[ \overline{X}\sim N(\mu,\frac{\sigma^2}{n}) \]

所以有

\[ Z=\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\sim N(0,1^2) \]

按照标准正态分布规律，95% 的 \(Z\) 值在 -1.96 和 1.96 之间，即

\[ P\left(-1.96\leqslant\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\leqslant1.96\right)=0.95 \]

展开有

\[ P\left(\overline{X}-1.96\frac{\sigma}{\sqrt{n}}\leqslant\mu\leqslant\overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right)=0.95 \]

即该种病人血浆纤维蛋白原含量总体均数的 95% 的置信区间为

\[ \left[\overline{X}-1.96\frac{\sigma}{\sqrt{n}}, \overline{X}+1.96\frac{\sigma}{\sqrt{n}}\right] \]

t 分布

但在实际中，总体标准差 \(\sigma\) 往往未知，通常用样本标准差 \(S\) 估计 \(\sigma\) ，

\[ t=\frac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}} \]

，但在这种情况下， \(t=\frac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}}\) 已不再服从标准正态分布，而是服从的 t 分布，t 分布的密度函数曲线如图所示，

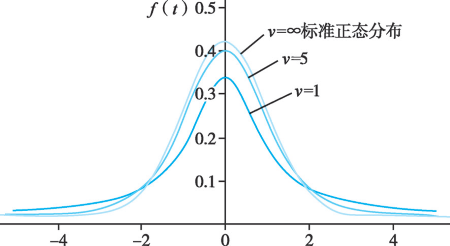
Figure 4. t 分布

由图可见，\(t\) 分布曲线的形态变化与自由度 \(\nu=n-1\) 有关。随着自由度 \(\nu\) 的增大，t 分布曲线越来越接近于标准正态分布曲线；当 \(\nu \to +\infty\) 时，t 分布的极限分布就是标准正态分布。

注：实际中，通常将样本量 \(n>50\) 的 t 分布近似视为正态分布。

因此，

\[ P\left(-t_{\alpha/2,\nu}\leqslant\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\leqslant t_{\alpha/2,\nu}\right)=1-\alpha \] 其中，

• \(\alpha \geq 0, t_{\alpha/2,\nu} \geq 0\)；
• \(t_{\alpha/2,\nu}\) 表示当自由度为 \(\nu\) 时，t 分布的密度曲线在 \(\pm t_{\alpha/2,\nu}\) 两侧曲线下面积为 \(\alpha\)，每侧均为 \(\alpha/2\)，即 \(P(x \leq -t_{\alpha/2,\nu}) = P(x \geq t_{\alpha/2,\nu}) =\alpha/2\).

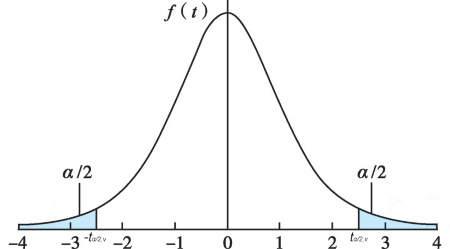
Figure 5. t 分布双侧面积

按 t 分布规律，\(100\%×(1−α)\) 的 \(t\) 值在 \(-t_{\alpha/2,\nu}\) 和 \(t_{\alpha/2,\nu}\) 之间，即

\[ P\left(-t_{\alpha/2,\nu}\leqslant\frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}\leqslant t_{\alpha/2,\nu}\right)=1-\alpha \]

因此置信区间表示为

\[ \left[\overline{X}-t_{\alpha/2,\nu}\frac{S}{\sqrt{n}}, \overline{X}+t_{\alpha/2,\nu}\frac{S}{\sqrt{n}}\right] \]

\(t_{\alpha/2,\nu}\) 值可以通过查表获得。

假设检验

假设检验（hypothesis test）亦称显著性检验（significance test），其目的是利用样本信息概率性地定性比较总体参数之间有无差别或总体分布是否相同。

如在比较甲乙两种治疗高脂血症药物疗效的试验中，甲乙两组各为 100 名患者，甲药使血清甘油三酯平均下降 1.36 mmol/L，乙药使血清甘油三酯平均下降 1.12 mmol/L，并不能简单判断甲药优于乙药。

两样本均数的不同可能是同一总体中抽样误差所致，也可能确实来自总体均数不同的两个总体。

假设检验的基本做法是，首先假设样本来自参数相等的同一个总体，然后通过样本数据去推断是否可以冒很小的风险去拒绝这一假设，从而回答样本统计量之间的不一致是否真正源于不同的总体。综上，假设检验主要利用了小概率和反证法两个基本思想。具体步骤由下面的例子说明。

某研究者从某工厂工人中随机抽取了 \(n\) 人，测量了血红蛋白含量，并计算出统计量均值 \(\overline{X}\) 和标准差 \(S\). 问该厂工人的血红蛋白是否不同于正常成年人血红蛋白平均值 \(\mu_0\)？

若该厂工人的血红蛋白与正常成年人血红蛋白平均值 \(\mu_0\) 相等，有

\[ H_0{:\ }\mu=\mu_0 \]

根据已知值 \(n, \overline{X}, S\) 构建统计检验量：

\[ t=\frac{\overline{X}-\mu}{\frac{S}{\sqrt{n}}} \]

因为有 \(\mu = \mu_0\)，所以

\[ t=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}} \]

若 \(\mu\rightarrow\mu_0\)，有 \(\overline{X}\approx\mu\rightarrow\mu_0\)，则 \(t\rightarrow0\)；即当 \(t\rightarrow0\)，有 \(\mu\approx\mu_0\)。即当 \(t\) 越靠近 \(0\) 时，工人所来自的总体的总体均数与正常成年人的总体均数越接近。

因为 \(t\) 服从 t 分布，\(t\) 离 \(0\) 越远时，其发生的概率也就越小；当 \(\lvert t \rvert\) 超过某一临界值 \(\lvert t_{\alpha/2,v} \rvert\) 时，\(t\) 几乎不会发生，即与原假设 \(H_0{:\ }\mu=\mu_0\) 相悖，因此也就越有把握认为 \(\mu\neq\mu_0\).

基本步骤

1. 先进行原假设：工人所来自的总体的总体均数与正常成年人的总体均数相等，

\[ H_0{:\ }\mu=\mu_0 \]

2. 否则接受备择假设：工人所来自的总体的总体均数与正常成年人的总体均数不相等，有

\[ H_1{:\ }\mu\neq\mu_0 \]

3. 建立两个检验假设的同时，还必须给出检验水准 \(\alpha\)。

检验水准亦称显著性水平（significance level），用 \(\alpha\) 表示，是预先规定的一个小概率值（通常取 \(0.05\) 或 \(0.01\)）.

4. 计算统计检验量 \(t\)，

\[ t=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}} \]

5. 当 \(\lvert t \rvert \geq \lvert t_{\alpha/2,v} \rvert\) 时，拒绝原假设，接受备择假设 \(H_1{:\ }\mu\neq\mu_0\)。即工人所来自的总体的总体均数与正常成年人的总体均数不相等。

也可以计算当自由度为 \(\nu\) 时，t 分布的密度曲线在 \(\pm t\) 双侧的曲线下面积 \(P(x \leq t, x \geq t)\)（即统计学软件给出的 P 值）。当 \(P \leq \alpha\)，拒绝原假设，接受备择假设。即工人所来自的总体的总体均数与正常成年人的总体均数在统计学上存在显著性差异。

需要注意的是，假设检验是通过反证法来确认两个总体间差异；当 \(P \geq \alpha\)，只能描述为“不拒绝 \(H_0\)”，并不等于两总体相同，只能说现有证据尚不能安全地给出两总体不同的结论。

单侧和双侧检验的选择

备择假设有双侧和单侧两种情况。上述的 \(H_1{:\ }\mu\neq\mu_0\) 即为双侧检验，当接受 \(H_1\) 时，\(t\) 位于 \(\pm t_{\alpha/2,\nu}\) 两侧。

单侧检验是指 \(H_1{:\ }\mu > \mu_0\)（或 \(H_1{:\ }\mu < \mu_0\)），当接受 \(H_1\) 时，\(t \geq \pm t_{\alpha,\nu}\) （或 \(t \leq -t_{\alpha,\nu}\) ）。

双侧检验和单侧检验的选择，需根据研究目的和专业知识而定。例如，比较两种降血脂药物的疗效，因无法判断两种药物的优劣，应选用双侧检验；如果是检验一种药物的疗效是否优于另一种阳性药物，这时可以采用单侧检验。如上述示例中，如果是检验该工厂工人的血红蛋白是否低于正常成年人血红蛋白平均值，则可采用单侧检测。

小结

除 t 分布外，针对不同的资料还有其他各种检验统计量及分布，如 F 分布、\(\chi^2\) 分布等，应用这些分布对不同类型的数据进行假设检验的步骤相同，其差别仅仅是需要计算的检验统计量不同。

后面会继续更新假设检验的具体方法，如 t 检验、方差分析、\(\chi^2\) 检验等，以及统计学的余下内容。

References

1. 李康, 贺佳. 医学统计学: 第8版[M]..北京: 人民卫生出版社, 2024. ISBN 9787117363310.

2. 美 伯恩斯坦 S,美 Bernstein Stephen,美 伯恩斯坦 R,等.统计学原理. 上册, 描述性统计学与概率[M].科学出版社,2002.

3. 伯恩斯坦.统计学原理:推断性统计学.下册[M].科学出版社,2002.