高效液相色谱方法的建立 01：分析方法开发

发表于 Waline：

HPLC 方法建立步骤

良好的系统适用性参数

一个好的分析方法，应该尽量满足：

  1. 目标峰分离度足够高（\(R_s \geq 2\)）；
  2. 保留因子 \(1<k<10\)；
  3. 总的分析时间 \(t_{Total} \leq 20\) min；
  4. 拖尾因子 \(T_f \to 1\) 且 \(T_f<2\)；
  5. 进样重现性（如：RSD 0.1%–0.25%）；
  6. 信噪比：\(S/N>10\)。

分离度

HPLC 法的基本条件应达到多组分的相互分离。根据分离度的定义式：

\[ R_{s} = \frac{2(t_{R2} - t_{R1})}{W_1 + W_2} \]

可知要分离得好，有两条途径：一是谱带窄，即柱效高；再就是谱带间距离大。

Purnell 方程

分离度 \(R_s\) 也用 Purnell 方程表示：

\[ R_s = \frac{\sqrt{N_2}}{4} \cdot \frac{(\alpha - 1)}{\alpha} \cdot \frac{k_2}{(k_2+1)} \]

假设 \(W_1 \approx W_2\)，可以在数学上证明：

\[ R_s = \frac{2(t_{R2}-t_{R1})}{W_1 + W_2} = \frac{\sqrt{N_2}}{4} \cdot \frac{(\alpha - 1)}{\alpha} \cdot \frac{k_2}{(k_2+1)} \]

具体证明如下：

\[ \begin{align*} R_s &= \frac{\sqrt{N}}{4} \cdot \frac{(\alpha - 1)}{\alpha} \cdot \frac{k_2}{(k_2+1)} \\ &=\frac{\sqrt{16 \left( \frac{t_{R2}}{W_2} \right)^2}}{4} \cdot \frac{\frac{k_2}{k_1}-1}{\frac{k_2}{k_1}} \cdot \frac{k_2}{k_2+1}\\ &=\frac{t_{R2}}{W_2} \cdot \frac{k_2-k_1}{k_2} \cdot \frac{k_2}{k_2+1}\\ &=\frac{t_{R2}}{W_2} \cdot \frac{k_2-k_1}{k_2+1}\\ &=\frac{t_{R2}}{W_2} \cdot \frac{\frac{t_{R2}-t_{0}}{t_{0}}-\frac{t_{R1}-t_{0}}{t_{0}}}{\frac{t_{R2}-t_{0}}{t_{0}}+1}\\ &=\frac{t_{R2}}{W_2} \cdot \frac{t_{R2}-t_{R1}}{t_{R2}}\\ &=\frac{t_{R2}-t_{R1}}{W_2}\\ \end{align*} \]

假设 \(W_1 \approx W_2\)，有：

\[ \begin{align*} R_s &= \frac{\sqrt{N_2}}{4} \cdot \frac{(\alpha - 1)}{\alpha} \cdot \frac{k_2}{(k_2+1)} \\ &=\frac{t_{R2}-t_{R1}}{W_2}\\ &=\frac{2(t_{R2}-t_{R1})}{W_1 + W_2}\\ \end{align*} \] 得证。

Purnell 方程也直接写成：

\[ R_s = \frac{2(t_{R2}-t_{R1})}{W_1 + W_2} = \frac{\sqrt{N}}{4} \cdot \frac{(\alpha - 1)}{\alpha} \cdot \frac{k}{(k+1)} \]

  • 保留值（Rention）：\(k\)
  • 选择性（Selectivity）：\(\alpha\)
  • 柱效（Efficiency）：\(N\)

将上述三项看作相互独立的参数，可以简化条件优化步骤。

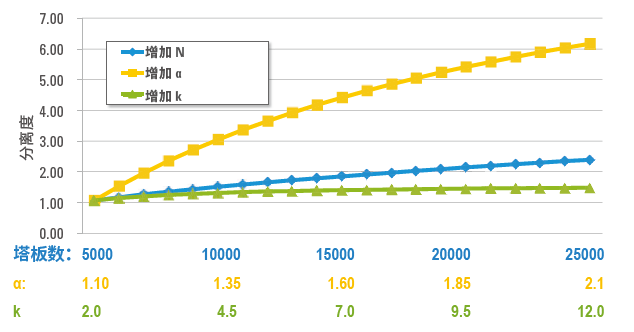
Figure 1. 保留因子（\(k\)）、选择性（\(\alpha\)）和塔板数（\(N\)）对分离度的影响

由上图可知，对分离度影响程度 \(\alpha > N > k\)。\(\alpha\) 项（即选择性）对分离度的影响远大于柱效和保留因子。因此，在方法开发过程中，改变选择性将对实现分离所需的分离度产生最大影响。

影响分离度的条件

Table 1. 不同的分离条件对保留因子（\(k\)）、选择性（\(\alpha\)）和塔板数（\(N\)）的影响

条件 \(k\) \(\alpha\) \(N\)
流动相的 pHa ++ ++ +
离子试剂浓度a, b ++ ++ +
色谱柱类型（C18、苯基、氰基等） + ++ -
B 溶剂（乙腈、甲醇等） + ++ -
%B ++ + -
温度 + + +
缓冲液浓度a + + -
柱长 0 0 ++
粒径 0 0 ++
流速 0 0 +
柱压 - - +c

注：++：主要影响；+：次要影响；-：相对影响很小；0：没有影响；加粗的量主要（和推荐）用于分别控制 \(k\)、\(\alpha\) 和 \(N\)。

a：适用于可电离的溶质分子（酸或碱）来说； b：在离子对色谱中尤其重要； c：通过适当选择其他分离条件，压力较高时，\(N\) 值也较高；然而压力本身对 \(N\) 的直接影响可以忽略不计。

pH 的影响

当分析物含有可电离官能团时，处于离子状态时的极性大，因此想要化合物在反相色谱上有更好的保留，化合物应该尽量不电离。

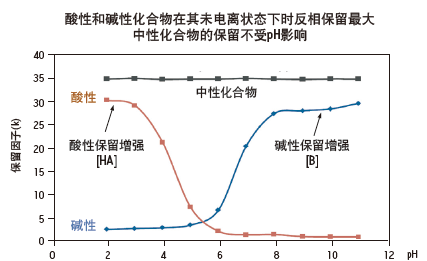
Figure 2. pH 对化合物保留的影响

对于酸性化合物

\[ \text{酸： }\mathrm{HA} \rightleftharpoons \mathrm{A}^{-} + \mathrm{H}^{+} \]

其电离常数

\[ K_a=\frac{[H^+][A^-]}{[HA]} \]

有

\[ pK_a=-\log_{10}K_{a} \]

对于碱性化合物

\[ \text{碱： }\mathrm{B} + \mathrm{H_{2}O} \rightleftharpoons \mathrm{BH}^{+} + \mathrm{OH}^{-} \]

其电离常数

\[ K_b=\frac{[BH^+][OH^-]}{[B]} \]

碱性化合物的 \(K_a\) 是其共轭酸的 \(K_a\)，即 \(K_a=\frac{[B][H^+]}{[BH^+]}\)，共轭酸碱对的电离常数乘积等于水的离子积常数（\(K_w\)）：

\[ K_a\cdot K_b=K_w=1.0\times10^{-14} \]

因此碱性化合物

\[ pK_a=14-pK_b \]

根据 \(\text{pK}_a\) 定义式，不难推导：当 \(\text{pH} = \text{pK}_a\) 时，化合物一半处于电离，一半处于非电离状态。常将 pH 设置在 \(pK_a \pm 2\) 以上，此时 99% 以上的化合物将分别处于电离或未电离状态。

如何选择合适的 pH？

logP 是反映化合物脂溶性的参数，通常 logP 越大的化合物，其非极性越大，在反相色谱柱上的保留能力也就越强。logD 是描述化合物在不同 pH 条件下脂溶性的参数，对于非中性化合物来讲，其脂溶性会随着 pH 发生变化。

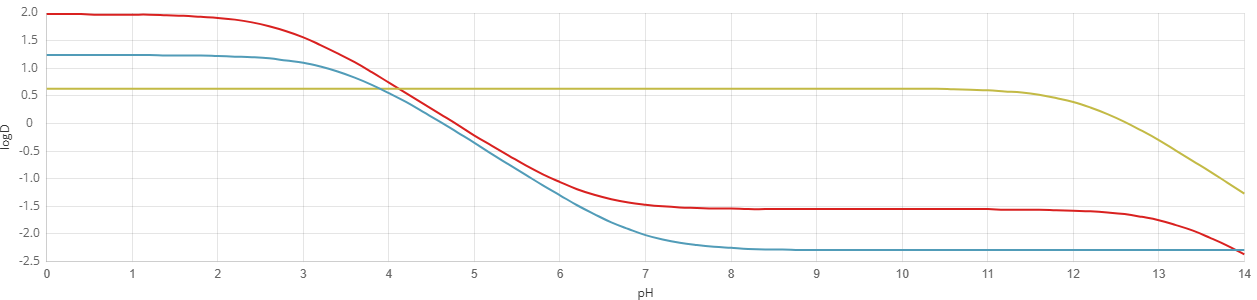
Figure 3. 某三种化合物的 logD-pH 关系图

上图是三种化合物的 logD-pH 关系图，可以看到在 \(pH \leq 2\) 时，三种化合物 logD 有较大的差异，有可能实现分离；且此时曲线也较为平缓，能够减少 pH 波动引起的重现性差。因此可以尝试设置 \(pH \leq 2\)。

Table 2. 常用的流动相 pH 调节剂

流动相化学成分 pKa 缓冲液范围 化学式 浓度为 10 mM 的流动相 (每 1 升) 所需的体积或质量 pH 调节 酸/碱 MS 兼容性
乙酸（冰醋酸） 4.8 – CH3COOH 0.571 mL – ✓
醋酸铵：pKa 1 4.8 3.8–5.8 CH3COONH4 0.770 g CH3COOH 或 NH4OH ✓
醋酸铵：pKa 2 9.2 8.2–10.2 CH3COONH4 0.770 g CH3COOH 或 NH4OH ✓
碳酸氢铵 9.2, 10.3 (8.2–11.3) NH4HCO3 0.790 g HCOOH 或 NH4OH ✓
碳酸铵 6.35, 9.25 5.9–6.9 和 8.8–9.8 (NH4)2CO3 0.961 g NH4OH ✓
甲酸铵：pKa 1 3.8 2.8–4.8 NH4COOH 0.640 g HCOOH 或 NH4OH ✓
甲酸铵：pKa 2 9.2 8.2–10.2 NH4COOH 0.640 g HCOOH 或 NH4OH ✓
氨水 9.2 – NH4OH 0.675 mL – ✓
磷酸氢二铵 7.2, 9.2 (6.2–10.2) (NH4)2HPO4 1.32 g H3PO4 或 NH4OH ×
甲酸 3.8 – HCOOH 0.420 mL – ✓
N-甲基吡咯烷 10.3 – C5H11NO 1.04 mL – ✓
磷酸 2.1 – H3PO4 0.580 mL – ×
磷酸二氢钾 2.1 (1.1–3.1) KH2PO4 1.36 g H3PO4 或 KOH ×
磷酸氢二钾 7.2 (6.2–8.2) K2HPO4 1.74 g H3PO4 或 KOH ×
磷酸钾 12.7 (11.7–13.7) K3PO4 2.12 g H3PO4 或 KOH ×
吡咯烷 11.3 – C4H9N 0.833 mL – ✓
硼酸钠 9.1, 12.7, 13.8 (8.2–14) Na2B4O7 2.01 g H3BO3 或 NaOH ×
柠檬酸三钠 3.1, 4.8, 6.4 (2.1–7.4) HOC(COONa)(CH2COONa)2 2.58 g 柠檬酸或 NaOH ×
三氟乙酸（TFA） 0.3 – CF3COOH 0.743 mL – ×

固定相的影响

固定相因其化学性质不同而会提供不同的保留与选择效果，色谱柱的选择可以参照“液相色谱柱”一文。

有机溶剂的影响

甲醇和乙腈，是用于反相色谱的典型有机溶剂。除了洗脱强度、粘度与柱背压有关、紫外吸收性不同，甲醇与乙腈在化学选择性上也有所不同，甲醇可以发生氢键作用，因此会提供显著不同的选择性。

甲醇

  • 洗脱能力较弱。
  • 质子化溶剂，提供氢键作用力，增强对化合物的洗脱能力，屏蔽硅醇基次级相互作用。
  • 截止波长比乙腈大（205 nm）

乙腈

  • 洗脱能力较强
  • 非质子化溶剂
  • 粘度较低（柱背压更低）
  • 截止波长更短（190 nm）

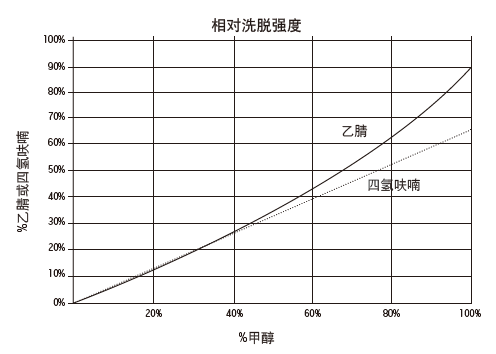
Figure 4. 有机溶剂相对洗脱强度曲线

梯度的影响

  • 更缓的梯度可以提高分离度，色谱峰会展宽，导致灵敏度下降；
  • 更陡的梯度斜率可能压缩色谱峰，灵敏度增加，经常会导致分离度的降低

改变梯度斜率时要平衡峰高与分离度的关系。

温度的影响

化合物保留随温度而变化的规律可以用下面这个等式描述：

\[ logk=A+B/T \]

  • \(A, B\)：对于给定的化合物是常数；
  • \(T\)：温度，单位 K。

因此温度的增加，会使化合物的保留 \(k\) 减小，引起选择性的改变（不一定是正向的）；此外温度增加能减少流动相粘度，降低背压。

pH 调节剂的影响

“缓冲容量”是指 pH 调节剂维持恒定 pH 的能力，取决于以下几点考虑：

  • pH 调节剂的 pKa 值；
  • pH 调节剂的浓度；
  • 流动相的 pH 值。

流动相的有效缓冲容量指的是当缓冲能力不足时，增加溶质的量并不会引起 pH 较大的变化。 以下的因素可以增加流动相的有效缓冲容量：

  1. 减少缓冲盐 pKa 值和流动相 pH 之间的差异（可调整 pH 或更换缓冲液）。
  2. 扩大流动相 pH 和溶质 pKa 值之间的差异（当差异足够大时，溶质被完全离子化或者保持非离子化形式，而此时，缓冲液就显得不重要了）。
  3. 增加缓冲液浓度。
  4. 减少样品进柱体积。
  5. 调节样品的 pH 与流动相的一致。

流动相的缓冲容量一般与缓冲液浓度成正比例关系，通常的浓度范围是 5–25 mM。

分析方法的建立

初始条件摸索

无论最终是采用等度洗脱还是梯度洗脱，都建议按照 Table 3 进行初始条件摸索。

Table 3. 初始条件参数

项目 类型 较好的初始条件
色谱柱a
尺寸（长度 × 内径 ID） 100 × 4.6 mm
粒度 3 μm
固定相 C8 或 C18
孔径 8–12 nm
流动相
溶剂 A 和 B 纯水（缓冲液）/乙腈
缓冲液 若有，水的缓冲液b（10–25 mM，pH2.5–3.0）
%B 10 min 内梯度 5%–100%a
流速 2.0 mL/mina
温度 30 °C 或 35 °C
样品
体积 \(\leq\) 50 μL
重量 \(\leq\) 10 μg
\(k^*\)c \(\approx\) 5

a：也可更换其他规格色谱柱，并使用下表推荐参数：

Table 4. Column volumes for various column configurations and recommended scouting gradient times

L (mm) dc (mm) Vm (mL) F (mL/min) tG (min) \(\Delta\phi\)
250 4.6 2.5 1.0 60 90%
150 4.6 1.6 2.0 20 90%
150 2.1 0.33 0.4 20 90%
100 4.6 1.0 2.0 10 90%
100 2.1 0.22 0.4 10 90%
50 2.1 0.11 0.5 5 90%

对于不在表中的参数可用下式换算：

\[ k^*=\frac{0.87t_{G}F}{V_m\Delta\phi S} \]

  • \(t_{G}\)：梯度时间，min；
  • \(F\)：流速，mL/min；
  • \(V_{m}\)：为色谱柱的死体积，mL；
  • \(\Delta\phi\)：%B 梯度变化范围，如乙腈从 5% 线性升到 95%，\(\Delta\phi = 90\%\)；
  • \(S\)：溶质敏感性常数（Solute Sensitivity Constant），用来描述溶质保留行为对流动相组成变化敏感程度的常数，对于小分子 \(S\) 大概在 4–5（常按 \(S \approx 4\) 估算），对于大分子 \(S\) 大概在 10–1000。

b：如 0.1% 的甲酸水溶液。

c：化合物在梯度洗脱过程中，从进入色谱柱到离开色谱柱，保留因子 \(k\) 是变化的，\(k^*\) 表示这段时间内 \(k\) 的平均值，\(k^*=\frac{0.87t_{G}F}{V_m\Delta\phi S}\)。

等度洗脱或梯度洗脱的选择

判断样品是否应该使用等度洗脱还是梯度洗脱：

\[ \Delta t_{R} = t_{-1} - t_1 \]

  • \(t_{-1}\)：最后一个目标峰的保留时间；
  • \(t_1\)：第一个目标峰的保留时间。

\(\frac{\Delta t_{R}}{t_{G}}\) 越小，表示全部色谱峰在某一浓度附近能够集中洗脱。

  • 当 \(\frac{\Delta t_{R}}{t_{G}} \leq 0.25\)：推荐使用等度洗脱；

  • 当 \(\frac{\Delta t_{R}}{t_{G}} \geq 0.40\)：推荐使用梯度洗脱。

对于 \(\frac{\Delta t_{R}}{t_{G}} \geq 0.10\)，也可以直接考虑梯度洗脱。

等度洗脱方法开发

若使用等度洗脱，等度洗脱的初始 %B 可以由下式进行估计：

\[ \%B \approx \frac{100\Delta\phi}{t_{G}}(t_{avg} - t_{D}) - 2 \]

  • \(t_{avg} = \frac{t_1 + t_{-1}}{2}\)，即第一个目标峰和最后一个目标峰保留时间的均值。
  • \(t_{D}\)：滞留时间。

使用确定好的 %B 对方法进行验证，流程如下图：

如何调整 %B

调整合适的流动相比例，使 \(1<k<10\)，按下式估算需要调节的比例：

\[ logk=logk_w-S\phi \]

  • \(k\)：保留因子。
  • \(logk\)：保留因子的对数。
  • \(logk_w\)：当流动相为 100% 水相时，该化合物的保留因子的对数，为理论值。
  • \(\phi\) ：流动相中有机相的体积分数。例如，如果流动相是 70% 甲醇和 30% 水，那么 \(\phi=0.7\)。
  • \(S\)：溶质敏感性常数（Solute Sensitivity Constant），用来描述溶质保留行为对流动相组成变化敏感程度的常数，对于小分子 \(S\) 大概在 4–5（常按 \(S \approx 4\) 估算），对于大分子 \(S\) 大概在 10–1000。

梯度洗脱方法开发

优化保留因子 \(k^*\)

\[ k^*=\frac{0.87t_{G}F}{V_m\Delta\phi S} \]

  • \(t_{G}\)：梯度时间，min；
  • \(F\)：流速，mL/min；
  • \(V_{m}\)：为色谱柱的死体积，mL;
  • \(\Delta\phi\)：%B 梯度变化范围，如乙腈从 5% 线性升到 95%，\(\Delta\phi = 90\%\)；
  • \(S\)：溶质敏感性常数（Solute Sensitivity Constant），用来描述溶质保留行为对流动相组成变化敏感程度的常数，对于小分子 \(S\) 大概在 4–5（常按 \(S \approx 4\) 估算），对于大分子 \(S\) 大概在 10–1000。

对于大多数的小分子样品（分子量 < 1000 Da）来说，Table 3 内推荐的其实梯度条件一般能够使他们的 \(k^*\) 平均值达到 \(\approx 5\)，因此通常无需再考虑优化 \(k^*\)。

优化梯度选择性 \(\alpha^*\)

越来越多的证据表明，在起始的方法试验中，梯度时间和温度是调整 \(\alpha\) 的首选变量，因此常对他们首先进行改变（同时保持 \(0.5 \leq k^* \leq 20\)）。

  1. 将梯度时间变为原来的 2–3 倍，同时保持 \(0.5 \leq k^* \leq 20\)。

  2. 通过改变温度，如增加 20 °C，查看分离是否得到改善。

  3. 以甲醇代替乙腈。

  4. 考虑更换色谱柱。

  5. 考虑使用分段梯度（由于不同仪器间的 \(t_D\) 不同，可能导致不同仪器间重现性差）

分析方法学开发流程

  1. 回顾样品信息

    • 被分析物数量：需要分离多少色谱峰？
    • 化合物化学结构（官能团）。
    • 化合物的分子量。
    • 化合物的 pKa。
    • 化合物的 UV 光谱。
    • 样品基质的性质：溶剂、填充物等。
    • 化合物在有关样品中的浓度范围和定量要求。
    • 样品的溶解度。
    • 样品需要预处理吗？
    • 流动相需要缓冲吗？

  2. 明确分离目的

    • 主要目的是分析还是回收样品组分？
    • 是否已知样品所有成分的化学特性，或是否需定性分析？
    • 是否有必要解析出样品的所有成分（比如对映体、非对映体、同系物、低聚物、痕量杂质）？
    • 如需定量分析，需精密度多高？
    • 本法需用于几种样品剂型（原料、制剂、环境样品等）？需要一种以上的 HPLC 方法吗？
    • 本法将仅用于分析几种样品，还是许多种？
    • 将使用最终方法的常规实验室中，已有哪些 HPLC 设备和技术？

  3. 运行起始分离条件

    • 按照 Table 3 中信息运行初始条件。
    • 有出现什么问题吗？
    • 可以使用等度分离吗？

  4. 优化梯度的保留因子 \(k^*\)（Table 3 内推荐的其实梯度条件一般能够使他们的 \(k^*\) 平均值达到 \(\approx 5\)，因此通常无需再考虑优化 \(k^*\)）

  5. 优化梯度选择性 \(\alpha^*\)

    • 将梯度时间变为原来的 2–3 倍，同时保持 \(0.5 \leq k^* \leq 20\)。
    • 通过改变温度，如增加 20 °C。
    • 以甲醇代替乙腈重复步骤 1–4。
    • 考虑更换色谱柱重复步骤 1–4。
    • 考虑使用分段梯度。

  6. 调整梯度范围和形状

    • 选择最佳的起始和最终的 %B，从而在分离度 \(R_s\) 合理的前提下实现最短的实验时间。
    • 对于“较脏的”样品，加入坡度较大的梯度分段至 100% B。
    • 加入梯度较大的梯度分段来加速色谱图后段的、间隔较宽的色谱峰的洗脱。
    • 加入等度停留从而改善梯度前段洗脱出来的色谱法之间的分离度。

  7. 以步骤 5 或 6 中获得的最佳的分离效果为基础，平衡分离度和运行时间

  8. 测量连续的样品进样之间，色谱柱的必要平衡时间

注：平衡时间需要优化，建议从 \(2t_0\) 开始。

下图是一个梯度洗脱程序示例：

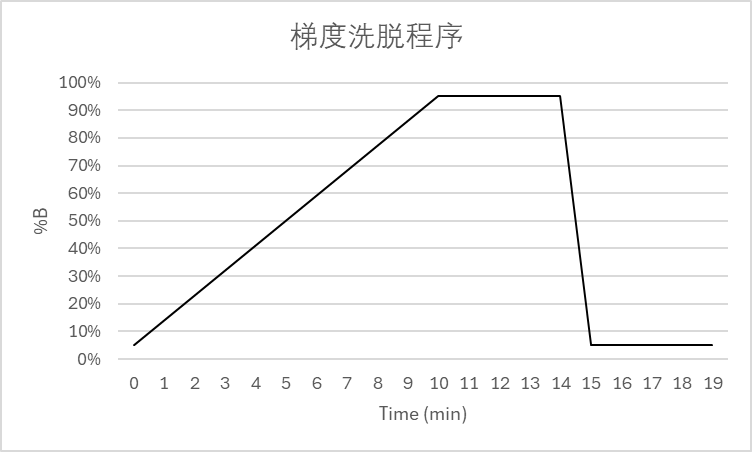
Figure 5. 梯度洗脱示例

Table 5. 梯度洗脱示例说明

Time (min) 说明
0–10 梯度洗脱
10–14 冲洗
14–15 将回到初始梯度浓度
15–19 平衡

References

  1. 斯奈德.实用高效液相色谱法的建立（第二版）[M].华文出版社,2001.

  2. Lloyd R. Snyder, Joseph J. Kirkland, John W. Dolan. 现代液相色谱技术导论[M]. 人民卫生出版社, 2012.

  3. “Making to the most of a Gradient Scouting Run” LCGC North America Vol. 31,Number 1, 2013.

  4. HPLC Method Development- From Beginner to Expert, Part 1: https://www.agilent.com/cs/library/slidepresentation/public/method-development-101-from-beginner-to-expert-part-1-feb202024.pdf

  5. 液相色谱手册：https://www.agilent.com/cs/library/primers/public/5990-7595CHCN.pdf

  6. 液相分析方法开发工具书：https://www.waters.com/content/dam/waters/zh/library/brochures/2015/720008028zh.pdf